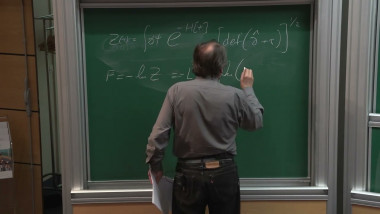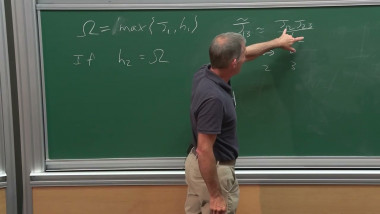100 (102!) Years of the Ising Model

Collection 100 (102!) Years of the Ising Model

Organizer(s) Hugo Duminil-Copin, Slava Rychkov, Béatrice de Tilière

Date(s) 30/05/2022 - 03/06/2022

linked URL https://indico.math.cnrs.fr/event/5466/

00:00:00 / 00:00:00

13 22

Nonperturbative analysis of noncritical Ising models: some applications of the Ornstein–Zernike theory

By Yvan Velenik

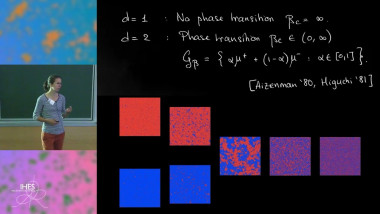
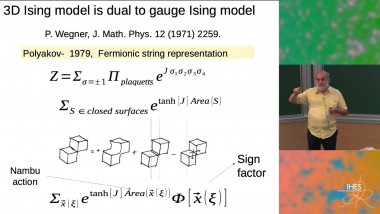
In its modern incarnation (developed during the last two decades), Ornstein-Zernike theory enables a non-perturbative analysis of non-critical ferromagnetic Ising models (and other models). I'll review some of its recent applications to the asymptotics of correlation functions (in any dimension) and to the fluctuation theory of interfaces (in the planar model).

Information about the video

Date of recording 01/06/2022
Date of publication 02/06/2022
Institution IHES
Language English
Audience Researchers
Format MP4

Domain(s)

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

01:06:55

published on June 1, 2022

The SLE/CLE continuum perspective on the two-dimensional critical Ising model

By Wendelin Werner

58:52

published on June 1, 2022

Non-self-averaging in the critical point of the 2D random Ising model

By Victor Dotsenko

33:14

published on June 1, 2022

The scaling limit of non-solvable 2D Ising models via fermionic RG - 1

By Alessandro Giuliani

32:07

published on June 1, 2022

The scaling limit of non-solvable 2D Ising models via fermionic RG - 2

By Rafael Greenblatt

01:02:19

published on June 1, 2022

On crossing probabilities in critical random-cluster models

By Eveliina Peltola

01:08:09

published on June 1, 2022

Random quantum Ising spin chains

By Daniel Fisher

55:36

published on June 1, 2022

Perspectives on the renormalisation group approach

By Roland Bauerschmidt

01:03:13

published on June 1, 2022

2D Ising Model and its tricritical version, when theory meets experiments

By Giuseppe Mussardo

51:03

published on June 1, 2022

Gibbs states for (long-range) Ising models

By Loren Coquille

01:08:13

published on June 2, 2022

Ising model, (para)fermions, and field theory

By Clément Hongler

01:05:14

published on June 2, 2022

Ising model, Glauber dynamics and random tilings

By Fabio Toninelli

59:31

published on June 2, 2022

Entropic repulsion in 3D Ising

By Eyal Lubetzky

01:07:42

published on June 2, 2022

Nonperturbative analysis of noncritical Ising models: some applications of the Ornstein–Zernike theory

By Yvan Velenik

01:03:06

published on June 3, 2022

Using the Ising model to explore the confining regime of Lattice Gauge Theories

By Michele Caselle

01:05:52

published on June 3, 2022

Three dimensional Ising model as a non-critical string theory

By Ara Sedrakyan

01:09:19

published on June 3, 2022

Metric graph extensions of lattice models with applications in stat mech and quantum systems

By Michael Aizenman

01:02:34

published on June 3, 2022

How the lizard got its colors

By Stanislav Smirnov

01:02:11

published on June 3, 2022

Ruminations on the Ising Model: Past, Present, Future

By Jürg Fröhlich , Tom Spencer , Arthur Jaffe , Geoffrey Grimmett , Joel Lebowitz

01:05:11

published on June 4, 2022

The Ising model, the saga of the critical exponents

By Jean Zinn-Justin

01:05:30

published on June 4, 2022

Emergent planarity in two-dimensional Ising models with finite-range Interactions

By Vincent Tassion

01:08:14

published on June 4, 2022

Anatomy of the Ising model from Conformal Bootstrap

By Alessandro Vichi

01:05:23

published on June 4, 2022

The multinomial Ising model

By Rick Kenyon

Copyright Carmin.tv 2024

Give feedback