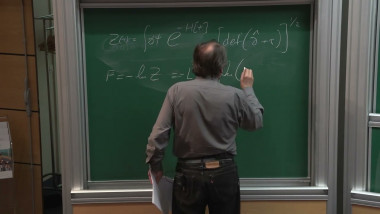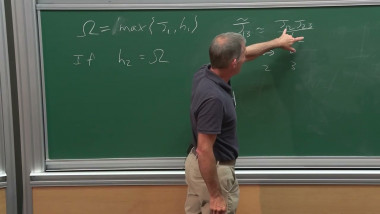The scaling limit of non-solvable 2D Ising models via fermionic RG - 1
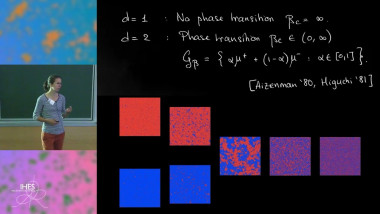
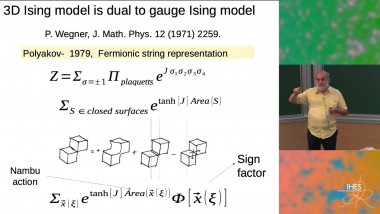
The scaling limit of any 2D Ising model with ferromagnetic short range interactions at the critical point is expected to be a Conformal Field Theory with c=1/2, one instance of which is the theory of free Majorana fermions. This expectation comes with extremely detailed predictions on critical exponents, on the form of the scaling limit of multipoint correlations and on their conformal covariance in finite domains. While the conjectured picture is now fully proved for nearest neighbor interactions, many open problems remain in the case of more general interactions. We will review the history of the problem and the state-of-the-art in the context of 2D Ising models with nearest neighbour interactions plus weak additional finite range interactions, focusing on results proved by rigorous fermionic Renormalization Group methods, and we will discuss perspectives and open problems. Based on joint works with Vieri Mastropietro.