An introduction to BSDE
Apparaît également dans la collection : CEMRACS - Summer school: Numerical methods for stochastic models: control, uncertainty quantification, mean-field / CEMRACS - École d'été : Méthodes numériques pour équations stochastiques : contrôle, incertitude, champ moyen
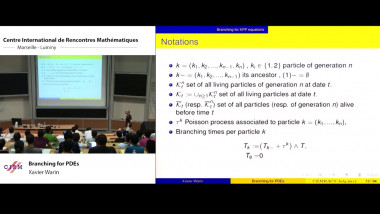
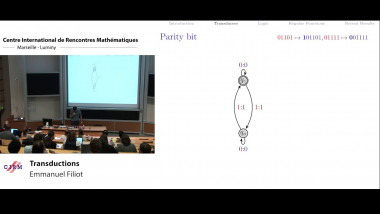
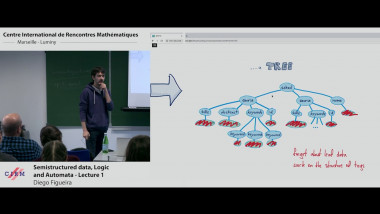
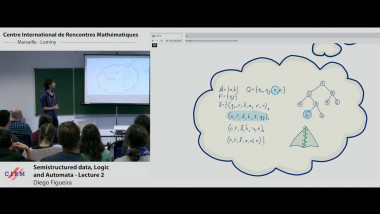
Backward stochastic differential equations have been a very successful and active tool for stochastic finance and insurance for some decades. More generally they serve as a central method in applications of control theory in many areas. We introduce BSDE by looking at a simple utility optimization problem in financial stochastics. We shall derive an important class of BSDE by applying the martingale optimality principle to solve an optimal investment problem for a financial agent whose income is partly affected by market external risk. We then present the basics of existence and uniqueness theory for solutions to BSDE the coefficients of which satisfy global Lipschitz conditions.