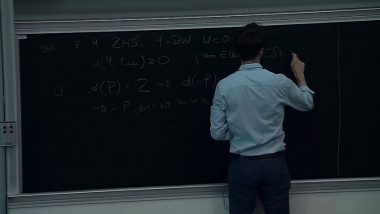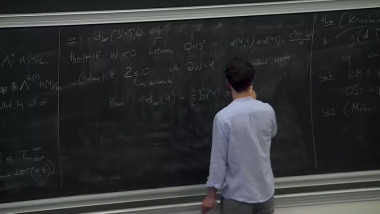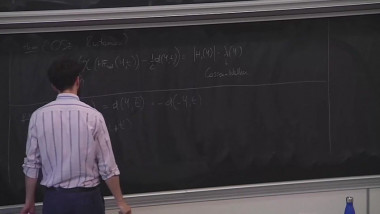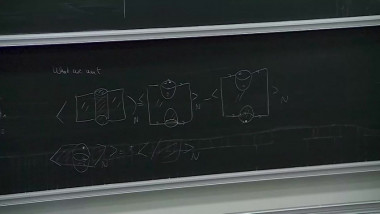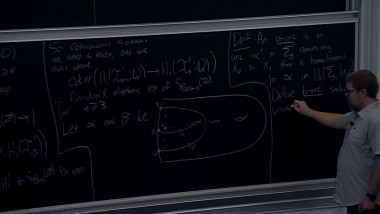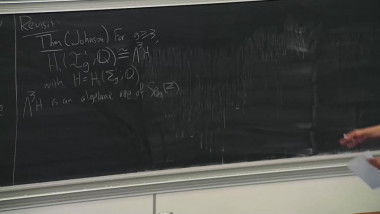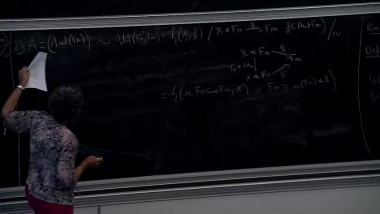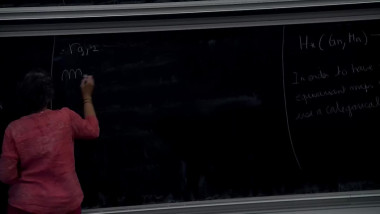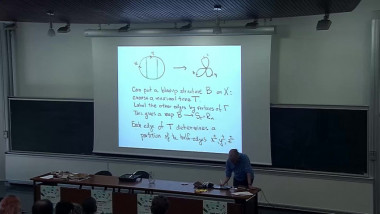Summer School 2024 - Low dimensional Topology

Collection Summer School 2024 - Low dimensional Topology

Organizer(s) Scientific Committee: Greg Kuperberg, Christine Lescop, Gwénaël Massuyeau, Jean-Baptiste Meilhan / Organization Committee: Christine Lescop, Gwénaël Massuyeau, Jean-Baptiste Meilhan

Date(s) 17/06/2024 - 05/07/2024

linked URL https://if-summer2024.sciencesconf.org

00:00:00 / 00:00:00

41 42

Profinite Rigidity and Colorings by Finite Quandles

By Darné Jacques

Quandles are algebraic structures introduced independently by Joyce and Matveev in 1982 for coloring knots and links. Specifically, any finite quandle Q induces a link invariant, which associates to a link L the number col(L,Q) of possible colorings of L by elements of Q. One might ask how precise these invariants are: given two distinct links L and L′, is there always a finite quandle Q such that col(L,Q) is different from col(L′,Q)? It is conjectured that this is the case, provided L′ cannot be obtained by taking the mirror image of a part of L. The aim of this talk is not to prove this difficult conjecture, but to show that it can be reformulated in terms closely related to classical questions of profinite rigidity. This will lead us to explore a bit of the theory of profinite quandles.

Information about the video

Date of recording 05/07/2024
Date of publication 07/01/2026
Institution Institut Fourier
Licence CC BY NC ND
Language English
Format MP4

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

01:06:06

published on January 7, 2026

Fukaya categories associated with graded surfaces and gentle algebras 4

By Claire Amiot

01:31:27

published on January 7, 2026

Fukaya categories associated with graded surfaces and gentle algebras 3

By Claire Amiot

01:39:08

published on January 7, 2026

Fukaya categories associated with graded surfaces and gentle algebras 2

By Claire Amiot

01:06:03

published on January 7, 2026

Fukaya categories associated with graded surfaces and gentle algebras 1

By Claire Amiot

01:06:10

published on January 7, 2026

Introduction to Heegaard-Floer homology 4

By Paolo Ghiggini

01:28:43

published on January 7, 2026

Introduction to Heegaard Floer homology 3

By Paolo Ghiggini

01:27:37

published on January 7, 2026

Introduction to Heegaard Floer homology 2

By Paolo Ghiggini

01:08:12

published on January 7, 2026

Introduction to Heegaard Floer homology 1

By Paolo Ghiggini

57:47

published on January 7, 2026

Surfaces in 4-manifolds 4

By Arunima Ray

01:23:23

published on January 7, 2026

Surfaces in 4-manifolds 3

By Arunima Ray

01:33:57

published on January 7, 2026

Surfaces in 4-manifolds 2

By Arunima Ray

01:07:52

published on January 7, 2026

Surfaces in 4-manifolds 1

By Arunima Ray

59:07

published on January 7, 2026

Khovanov invariants via immersed curves 4

By Liam Watson

01:34:18

published on January 7, 2026

Khovanov invariants via immersed curves 3

By Liam Watson

01:25:15

published on January 7, 2026

Khovanov invariants via immersed curves 2

By Liam Watson

01:06:50

published on January 7, 2026

Khovanov invariants via immersed curves 1

By Liam Watson

01:02:09

published on January 7, 2026

Applications of Heegaard Floer homology 4

By Marco Golla

01:20:11

published on January 7, 2026

Applications of Heegaard Floer homology 3

By Marco Golla

01:30:20

published on January 7, 2026

Applications of Heegaard Floer homology 2

By Marco Golla

01:05:04

published on January 7, 2026

Applications of Heegaard Floer homology 1

By Marco Golla

01:01:10

published on January 7, 2026

Foam lectures on link homologies 4

By Emmanuel Wagner

01:31:50

published on January 7, 2026

Foam lectures on link homologies 3

By Emmanuel Wagner

01:35:09

published on January 7, 2026

Foam lectures on link homologies 2

By Emmanuel Wagner

58:46

published on January 7, 2026

Foam lectures on link homologies 1

By Emmanuel Wagner

01:01:38

published on January 7, 2026

The topology of the mapping class group and its Torelli subgroup 4

By Andrew Putman

01:00:02

published on January 7, 2026

The topology of the mapping class group and its Torelli subgroup 3

By Andrew Putman

58:12

published on January 7, 2026

The topology of the mapping class group and its Torelli subgroup 2

By Andrew Putman

52:30

published on January 7, 2026

The Steinberg representations

By Andrew Putman

01:02:56

published on January 7, 2026

The topology of the mapping class group and its Torelli subgroup 1

By Andrew Putman

01:01:15

published on January 7, 2026

Homological stability and stable homology 3

By Christine Vespa

01:03:50

published on January 7, 2026

Homological stability and stable homology 2

By Christine Vespa

01:01:48

published on January 7, 2026

Homological stability and stable homology 1

By Christine Vespa

01:02:35

published on January 7, 2026

On the properties of quantum representations of mapping class groups of surfaces 4

By Renaud Detcherry

01:04:01

published on January 7, 2026

On the properties of quantum representations of mapping class groups of surfaces 3

By Renaud Detcherry

59:10

published on January 7, 2026

On the properties of quantum representations of mapping class groups of surfaces 2

By Renaud Detcherry

01:03:46

published on January 7, 2026

On the properties of quantum representations of mapping class groups of surfaces 1

By Renaud Detcherry

01:01:03

published on January 7, 2026

Finite groups of outer automorphisms of right-angled Artin groups

By Karen Vogtmann

01:00:38

published on January 7, 2026

Automorphism groups of Artin groups of spherical type

By Luis Paris

01:00:34

published on January 7, 2026

Stable homology of the IA-automorphism group

By Mai Katada

01:04:55

published on January 7, 2026

Non-semisimple quantum representations of mapping class groups

By Marco de Renzi

01:01:35

published on January 7, 2026

Profinite Rigidity and Colorings by Finite Quandles

By Darné Jacques

56:25

published on January 7, 2026

Mapping class groups and 4-manifolds

By Louis Funar

Copyright Carmin.tv 2026

Give feedback