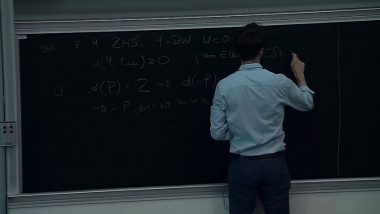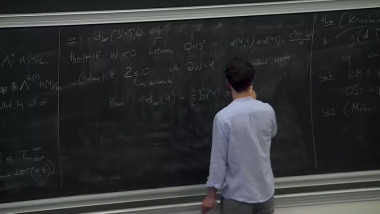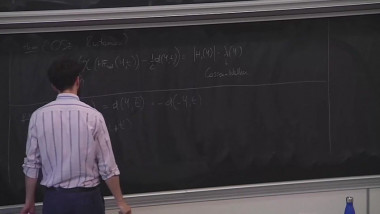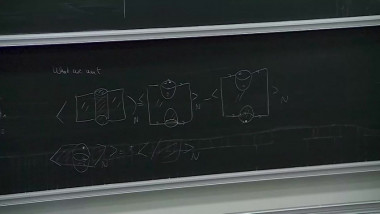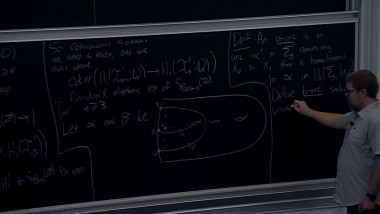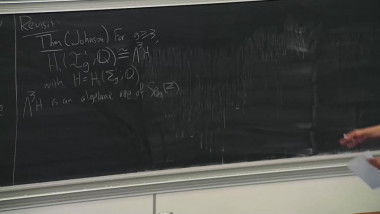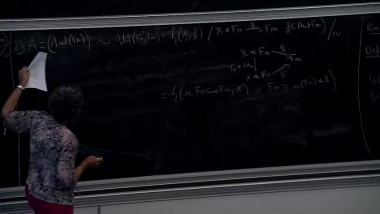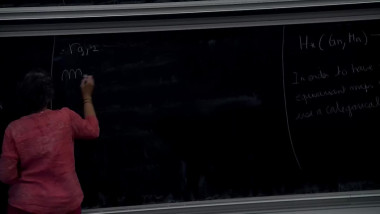Summer School 2024 - Low dimensional Topology

Collection Summer School 2024 - Low dimensional Topology

Organizer(s) Scientific Committee: Greg Kuperberg, Christine Lescop, Gwénaël Massuyeau, Jean-Baptiste Meilhan / Organization Committee: Christine Lescop, Gwénaël Massuyeau, Jean-Baptiste Meilhan

Date(s) 17/06/2024 - 05/07/2024

linked URL https://if-summer2024.sciencesconf.org

00:00:00 / 00:00:00

9 42

Surfaces in 4-manifolds 4

In this minicourse we will survey what is known about surfaces in 4-manifolds: their existence, their uniqueness, and their various properties. We will be especially interested in the question of when a given map of a surface to a 4-manifold is homotopic to a locally flat embedding. I will outline two fruitful approaches to this problem. The first is to use an analogue of Freedman's disc embedding theorem, generalised to arbitrary compact surfaces in joint work with Kasprowski, Powell, and Teichner. The second approach uses topological surgery theory, due to Freedman and Quinn.

Information about the video

Date of recording 21/06/2024
Date of publication 07/01/2026
Institution Institut Fourier
Licence CC BY NC ND
Language English
Format MP4

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

01:06:06

published on January 7, 2026

Fukaya categories associated with graded surfaces and gentle algebras 4

By Claire Amiot

01:31:27

published on January 7, 2026

Fukaya categories associated with graded surfaces and gentle algebras 3

By Claire Amiot

01:39:08

published on January 7, 2026

Fukaya categories associated with graded surfaces and gentle algebras 2

By Claire Amiot

01:06:03

published on January 7, 2026

Fukaya categories associated with graded surfaces and gentle algebras 1

By Claire Amiot

01:06:10

published on January 7, 2026

Introduction to Heegaard-Floer homology 4

By Paolo Ghiggini

01:28:43

published on January 7, 2026

Introduction to Heegaard Floer homology 3

By Paolo Ghiggini

01:27:37

published on January 7, 2026

Introduction to Heegaard Floer homology 2

By Paolo Ghiggini

01:08:12

published on January 7, 2026

Introduction to Heegaard Floer homology 1

By Paolo Ghiggini

57:47

published on January 7, 2026

Surfaces in 4-manifolds 4

By Arunima Ray

01:23:23

published on January 7, 2026

Surfaces in 4-manifolds 3

By Arunima Ray

01:33:57

published on January 7, 2026

Surfaces in 4-manifolds 2

By Arunima Ray

01:07:52

published on January 7, 2026

Surfaces in 4-manifolds 1

By Arunima Ray

59:07

published on January 7, 2026

Khovanov invariants via immersed curves 4

By Liam Watson

01:34:18

published on January 7, 2026

Khovanov invariants via immersed curves 3

By Liam Watson

01:25:15

published on January 7, 2026

Khovanov invariants via immersed curves 2

By Liam Watson

01:06:50

published on January 7, 2026

Khovanov invariants via immersed curves 1

By Liam Watson

01:02:09

published on January 7, 2026

Applications of Heegaard Floer homology 4

By Marco Golla

01:20:11

published on January 7, 2026

Applications of Heegaard Floer homology 3

By Marco Golla

01:30:20

published on January 7, 2026

Applications of Heegaard Floer homology 2

By Marco Golla

01:05:04

published on January 7, 2026

Applications of Heegaard Floer homology 1

By Marco Golla

01:01:10

published on January 7, 2026

Foam lectures on link homologies 4

By Emmanuel Wagner

01:31:50

published on January 7, 2026

Foam lectures on link homologies 3

By Emmanuel Wagner

01:35:09

published on January 7, 2026

Foam lectures on link homologies 2

By Emmanuel Wagner

58:46

published on January 7, 2026

Foam lectures on link homologies 1

By Emmanuel Wagner

01:01:38

published on January 7, 2026

The topology of the mapping class group and its Torelli subgroup 4

By Andrew Putman

01:00:02

published on January 7, 2026

The topology of the mapping class group and its Torelli subgroup 3

By Andrew Putman

58:12

published on January 7, 2026

The topology of the mapping class group and its Torelli subgroup 2

By Andrew Putman

52:30

published on January 7, 2026

The Steinberg representations

By Andrew Putman

01:02:56

published on January 7, 2026

The topology of the mapping class group and its Torelli subgroup 1

By Andrew Putman

01:01:15

published on January 7, 2026

Homological stability and stable homology 3

By Christine Vespa

01:03:50

published on January 7, 2026

Homological stability and stable homology 2

By Christine Vespa

01:01:48

published on January 7, 2026

Homological stability and stable homology 1

By Christine Vespa

01:02:35

published on January 7, 2026

On the properties of quantum representations of mapping class groups of surfaces 4

By Renaud Detcherry

01:04:01

published on January 7, 2026

On the properties of quantum representations of mapping class groups of surfaces 3

By Renaud Detcherry

59:10

published on January 7, 2026

On the properties of quantum representations of mapping class groups of surfaces 2

By Renaud Detcherry

01:03:46

published on January 7, 2026

On the properties of quantum representations of mapping class groups of surfaces 1

By Renaud Detcherry

01:01:03

published on January 7, 2026

Finite groups of outer automorphisms of right-angled Artin groups

By Karen Vogtmann

01:00:38

published on January 7, 2026

Automorphism groups of Artin groups of spherical type

By Luis Paris

01:00:34

published on January 7, 2026

Stable homology of the IA-automorphism group

By Mai Katada

01:04:55

published on January 7, 2026

Non-semisimple quantum representations of mapping class groups

By Marco de Renzi

01:01:35

published on January 7, 2026

Profinite Rigidity and Colorings by Finite Quandles

By Darné Jacques

56:25

published on January 7, 2026

Mapping class groups and 4-manifolds

By Louis Funar

Copyright Carmin.tv 2026

Give feedback