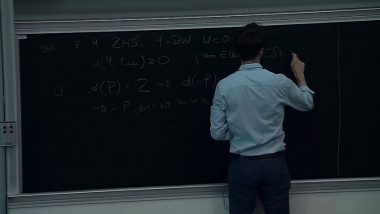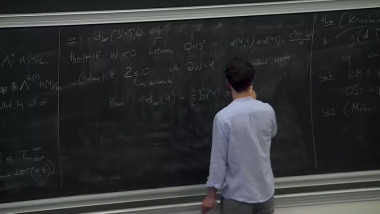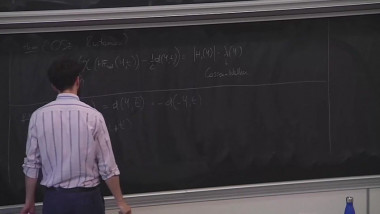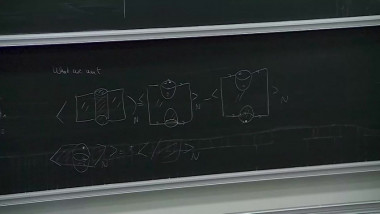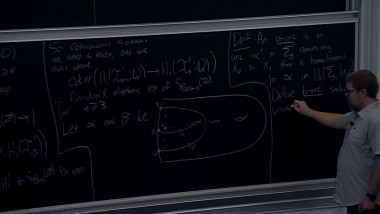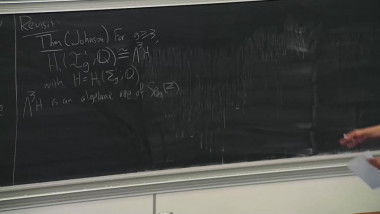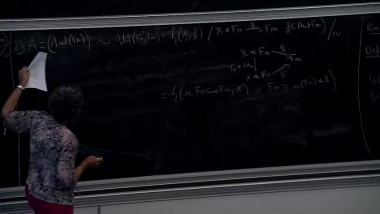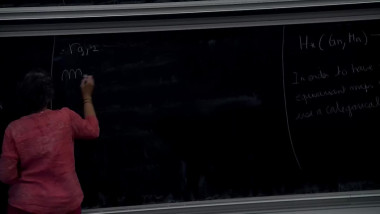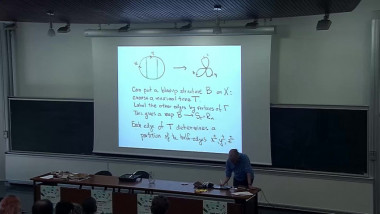Carmin.tv

Mathematics
and Interactions

Please leave your feedback in order for us to improve your experience !
Takeshi Saito : Singular Supports in Equal and Mixed Characteristics
4 videos

Takeshi Saito : Singular Supports in Equal and Mixed Characteristics

Summer School 2024 - Low dimensional Topology
42 videos

Summer School 2024 - Low dimensional Topology

Summer School 2023 - New trends in mathematical fluid dynamics
31 videos

Summer School 2023 - New trends in mathematical fluid dynamics

Emergent phenomena in many-body quantum systems / Phénomènes émergents des systèmes quantiques a plusieurs corps
5 videos

Emergent phenomena in many-body quantum systems / Phénomènes émergents des systèmes quantiques a plusieurs corps

All the collections
CIMPA
CIRM
IHES
IHP
Institut Fourier
LMR
SMF
All the institutions
Summer School 2024 - Low dimensional Topology

Collection Summer School 2024 - Low dimensional Topology

Organizer(s) Scientific Committee: Greg Kuperberg, Christine Lescop, Gwénaël Massuyeau, Jean-Baptiste Meilhan / Organization Committee: Christine Lescop, Gwénaël Massuyeau, Jean-Baptiste Meilhan
Date(s) 17/06/2024 - 05/07/2024
linked URL https://if-summer2024.sciencesconf.org
00:00:00 / 00:00:00
2 42

Fukaya categories associated with graded surfaces and gentle algebras 3

By Claire Amiot

To a graded surface (i.e. surface endowed with a line field), and with marked points on its boundary, Haiden, Katzarkov and Kontsevich have associated in 2014 a certain A_infinity category called the partially wrapped Fukaya category. This series of lectures will focus on this construction and its links with the derived categories of gentle algebras. In a first part, I will give the definition of A-infinity categories, and illustrate this notion with the A-infinity structure of the category given by a system of graded arcs on a graded surface which can be understood combinatorially. In a second part, I will explain the construction of twisted complexes of A-infinity categories and how two systems of graded arcs on the same surface give rise to a Morita equivalence. In a third part, I will explain the notion of formal generator, and give the link with gentle algebras. Finally, I will explain how to generalize these constructions for certain graded orbifolds, which is a collaboration with Pierre-Guy Plamondon.

Information about the video

  • Date of recording 20/06/2024
  • Date of publication 07/01/2026
  • Institution Institut Fourier
  • Licence CC BY NC ND
  • Language English
  • Format MP4

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow




Register

  • Bookmark videos
  • Add videos to see later &
    keep your browsing history
  • Comment with the scientific
    community
  • Get notification updates
    for your favorite subjects
Copyright Carmin.tv 2026
By browsing our website, you accept the use of cookies to improve your experience. Find out more about our privacy policy.
Approve
Give feedback