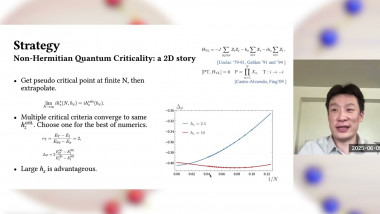
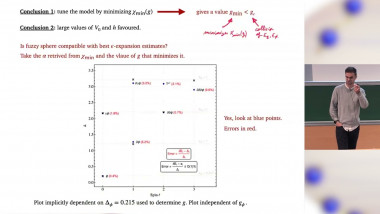
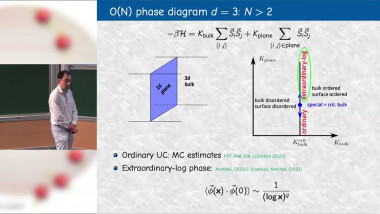
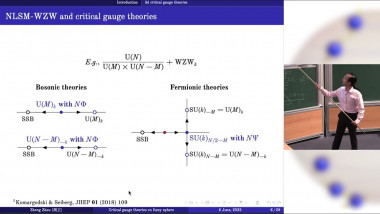
Yang-Lee criticality is the simplest non-Hermitian conformal field theory. The model was first reported as a phase transition of Ising model in imaginary longitudinal magnetic field more than half a centry ago. Since then, many qualitative and quantitative properties of YL criticality have been studied, remarkably, including the fact that the model can be described in Landau-Ginzburg scheme with a scalar $i\phi^3$ theory in $D<6$ and the fact that the 2D version is an exactly solvable minimal model. In higher dimensions, the model lacks the same level of understanding as the Ising criticality due to its non-Hermitian nature. We report a new study of 3D YL criticality as a phase transition of Fuzzy Sphere model, which facilitates a direct survey of many quantities such as the spectrum and OPE coefficient to high precision. These quantitative results show a beautiful agreement with conformal symmetry and previous estimates from $(6-\epsilon)$ expansion and conformal bootstrap. We also study YL model in 3D and 4D regular polytopes and obtained qualitative agreement with other methods.