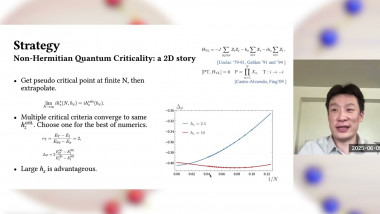
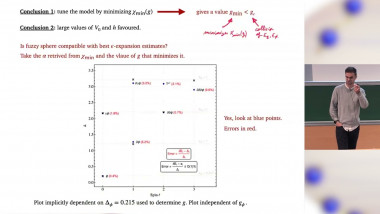
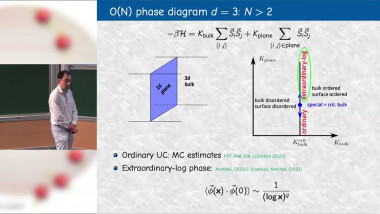
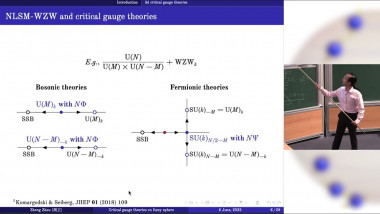
Fuzzy Sphere, Conformal Generators, and Ising Field Theory
In this talk, I will present recent results on constructing conformal generators on the fuzzy sphere for the 3D Ising conformal field theory. Our approach builds translations and special conformal transformations directly from the Hamiltonian density and as a result requires additional tuning to suppress contributions from irrelevant operators and their descendants. I will show how these improved generators can be used to accurately isolate primary operators. In the second part of the talk, I will discuss deformations by the lowest Z2-odd relevant operator, which defines the so-called Ising Field Theory. This deformation is especially rich and well studied in two dimensions, and I will present new results that emerge in the 3D setting.