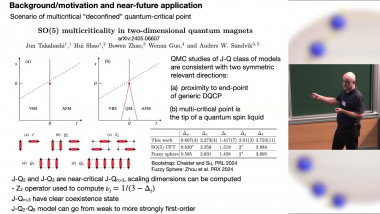
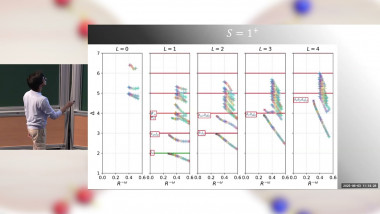
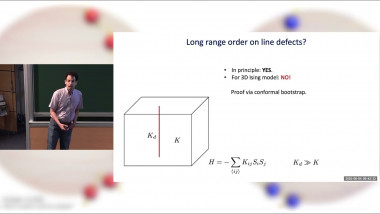
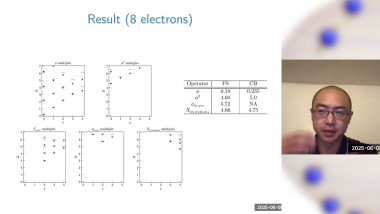
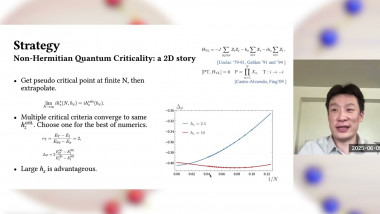
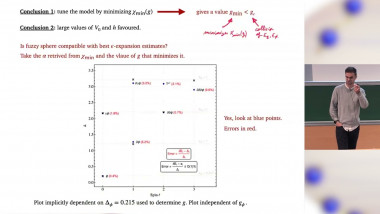
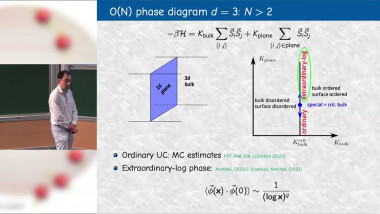
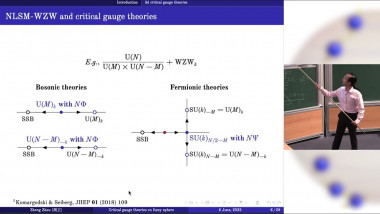
An Upper Bound on the Thermal Mass Gap at Criticality
An intrinsic quantity characterizing a scale-invariant quantum field theory (SFT) is its thermal mass gap, controlling its correlation length at finite temperature. By scale-invariance, this is a pure number in units of the temperature. For 2+1d SFTs, one way to probe the thermal mass gap is via the Casimir energy on a two-torus. Using a certain positivity assumption on the torus Casimir energy that I will motivate, in addition to extra constraints coming from modular invariance, I will show that the thermal mass gap is bounded from above within the class of theories satisfying the positivity constraint, independent of any other theory-dependent data. As a by-product, I will obtain bounds on the shape-dependence of the torus Casimir energy and will study a solution saturating the bounds.