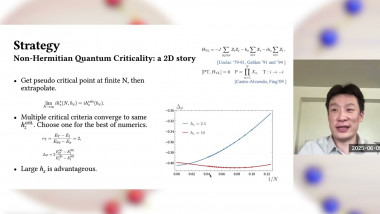
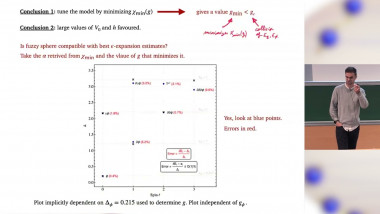
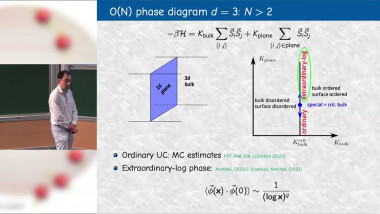
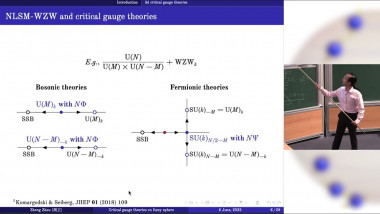
Multiple scaling dimensions from operator covariance in Monte Carlo simulations
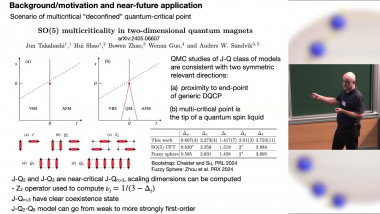
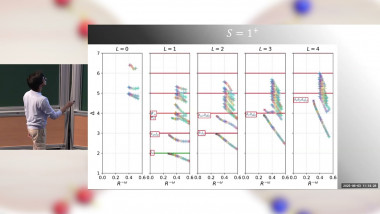
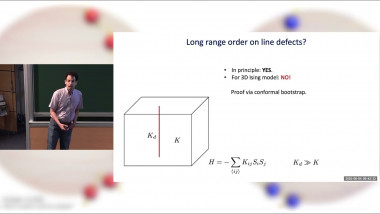
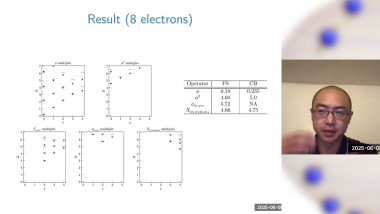
In classical and quantum Monte Carlo simulations of critical systems, the focus is often on the standard critical exponents, which correspond to the relevant scaling dimensions of the underlying continuum field theory. I will discuss a method by which multiple scaling dimensions can be computed efficiently bu diagonalizing a covariance matrix. While such an approach is common for extracting low-lying levels in the spectrum of a Hamiltonian, I show that the eigenvalues also disentangle scaling dimensions in the regime where they exhibit power-law decays. I will illustrate the method with the 2D and 3D classical Ising models, the Blume-Capel model at its tricritical point, as well as 1D quantum systems. The method should be useful for further studying what appears to be an SO(5) "deconfined" multi-critical point in the setting of J-Q models.