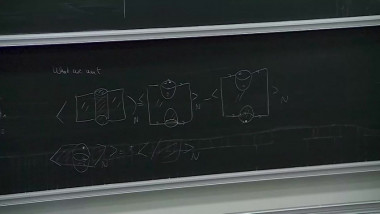Carmin.tv

Mathématiques
et Interactions

Merci de nous donner votre avis pour que nous puissions améliorer votre expérience !
Takeshi Saito : Singular Supports in Equal and Mixed Characteristics
4 videos

Takeshi Saito : Singular Supports in Equal and Mixed Characteristics

Summer School 2024 - Low dimensional Topology
42 videos

Summer School 2024 - Low dimensional Topology

Summer School 2023 - New trends in mathematical fluid dynamics
31 videos

Summer School 2023 - New trends in mathematical fluid dynamics

Emergent phenomena in many-body quantum systems / Phénomènes émergents des systèmes quantiques a plusieurs corps
5 videos

Emergent phenomena in many-body quantum systems / Phénomènes émergents des systèmes quantiques a plusieurs corps

Toutes les collections
CIMPA
CIRM
IHES
IHP
Institut Fourier
LMR
SMF
Tous les instituts
Summer School 2024 - Low dimensional Topology

Collection Summer School 2024 - Low dimensional Topology

Organisateur(s) Scientific Committee: Greg Kuperberg, Christine Lescop, Gwénaël Massuyeau, Jean-Baptiste Meilhan / Organization Committee: Christine Lescop, Gwénaël Massuyeau, Jean-Baptiste Meilhan
Date(s) 17/06/2024 - 05/07/2024
URL associée https://if-summer2024.sciencesconf.org
00:00:00 / 00:00:00
14 42

Khovanov invariants via immersed curves 3

De Liam Watson

Both Heegaard Floer homology and Khovanov homology admit relative versions associated with surface decompositions. In the case of a manifold with torus boundary, the Heegaard Floer invariant can be Both Heegaard Floer homology and Khovanov homology admit relative versions associated with surface decompositions. In the case of a manifold with torus boundary, the Heegaard Floer invariant can be interpreted in terms of immersed curves in a punctured torus; and in the case of a 4-ended tangle, the Khovanov invariant can be interpreted in terms of immersed curves in the 4-punctured sphere. While these invariants have different origins, this point of view highlights common algebraic underpinnings. Using mutation as a point of departure, this series will focus on Khovanov invariants in order to tell some of the algebraic and the geometric parts of this story.Lecture 1 (1 hour): Conway's mutation problemLecture 2 (1.5 hours): Bar-Natan's category from a bordered perspectiveLecture 3 (1.5 hours): Tangle invariants as immersed curvesLecture 4 (1 hour): Linearity: towards mutation invariance over any field

Informations sur la vidéo

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow




Inscrivez-vous

  • Mettez des vidéos en favori
  • Ajoutez des vidéos à regarder plus tard &
    conservez votre historique de consultation
  • Commentez avec la communauté
    scientifique
  • Recevez des notifications de mise à jour
    de vos sujets favoris
Copyright Carmin.tv 2026
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour améliorer votre expérience. En savoir plus sur notre politique de confidentialité.
Accepter
Donner son avis