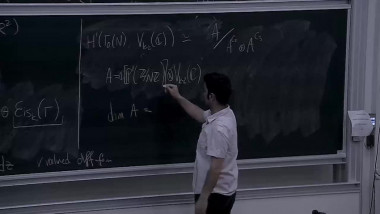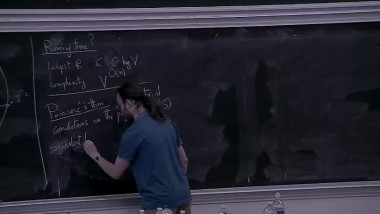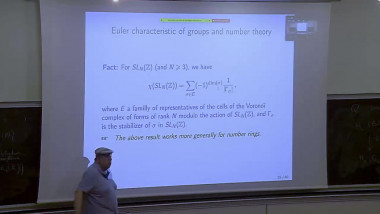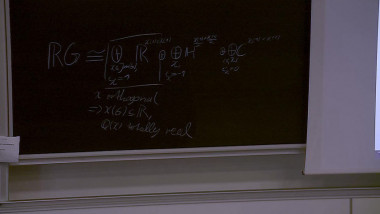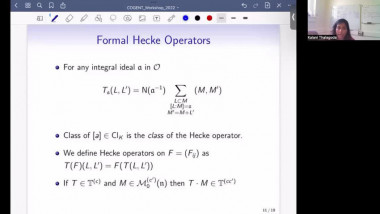
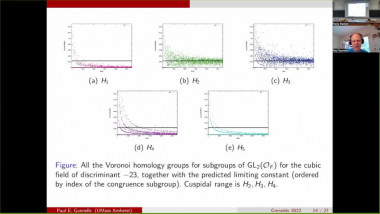
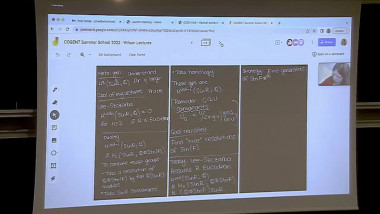
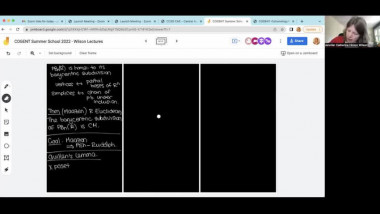
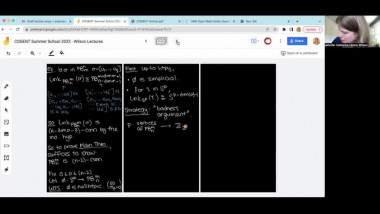
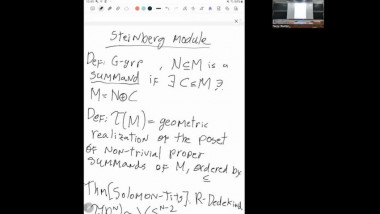
Summer School of mathematics 2022By a result of Church-Putman, the rational cohomology of $\operatorname{SL}_n(\mathbb{Z})$ vanishes in "codimension one", i.e. $H^{{n \choose 2} -1}(\operatorname{SL}_n(\mathbb{Z});\mathbb{Q}) = 0$ for $n \geq 3$, where ${n \choose 2}$ is the virtual cohomological dimension of $\operatorname{SL}_n(\mathbb{Z})$. I will talk about work in progress on two generalisations of this result: The first project is joint work with Miller-Patzt-Sroka-Wilson (see https://arxiv.org/abs/2204.11967). We show that the rational cohomology of $\operatorname{SL}_n(\mathbb{Z})$ vanishes in codimension two, i.e. $H^{{n \choose 2} -2}(\operatorname{SL}_n(\mathbb{Z});\mathbb{Q}) = 0$ for $n \geq 3$. The second project is joint with Patzt-Sroka. Its aim is to study whether the rational cohomology of the symplectic group $\operatorname{Sp}_{2n}(\mathbb{Z})$ vanishes in codimension one, i.e. whether $H^{n^2 -1}(\operatorname{Sp}_{2n}(\mathbb{Z});\mathbb{Q}) = 0$ for $n \geq 2$.
By Mehmet Haluk Sengun
By Mehmet Haluk Sengun
By Aurel Page
By Alexander Hulpke
By Alexander Hulpke
By Alexander Hulpke
By Paul Gunnells
By Aurel Page
By Peter Patzt
By Peter Patzt
By Peter Patzt
By Jennifer Wilson
By Jennifer Wilson
By Jennifer Wilson
By Haowen Zhang
By Renaud Coulangeon
By Renaud Coulangeon
By Bill Allombert
By Lewis Combes
By Alexander Hulpke
By Alexander Hulpke
By Paul Gunnells
By Paul Gunnells
By Paul Gunnells
By Paul Gunnells
By Graham Ellis
By Graham Ellis
By Graham Ellis
By Graham Ellis
By Graham Ellis
By Philippe Elbaz-Vincent
By Philippe Elbaz-Vincent
By Philippe Elbaz-Vincent
By Bettina Eick
By Petru Constantinescu
By Angelica Babei
By Alexander, D. Rahm
By Benjamin Brück
By Calista Bernard
By Philippe Elbaz-Vincent
By Bettina Eick
By Bettina Eick
By Bettina Eick
By Bettina Eick
By Herbert Gangl
By Zachary Himes
By Etienne Ghys
By Gergerly Bérczi
