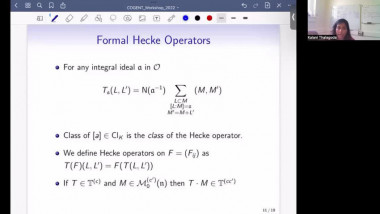
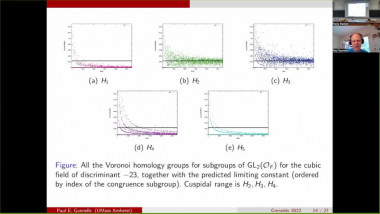
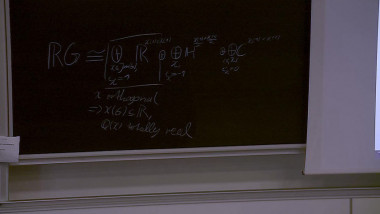Hilbert series and mild groups
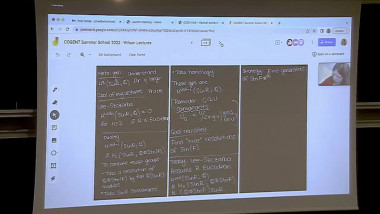
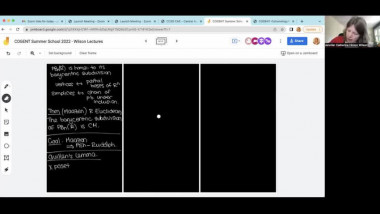
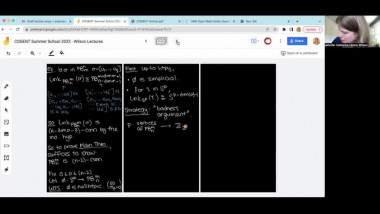
Let $p$ be an odd prime number and $G$ a finitely generated pro-$p$ group. Define $I(G)$ the augmentation ideal of the group algebra of $G$ over $F_p$ and define the Hilbert series of $G$ by: $G(t):=sum_{n\in \NN} \dim_{\F_p} I^n(G)/I^{n+1}(G)$.The series $G(t)$ gives several information on $G$. First, during the $60$'s, Golod and Shafarevich used Hilbert series to relate the number of generators and relations defining $G$, to the cardinality of $G$. Also, if $G(t)$ satisfies some equalities, we can read the cohomological dimension of $G$. Between 1980 and 2000's, Anick and Labute, introduced a sufficient and easy condition on the relations of pro-$p$-group $G$, such that $G(t)$ satisfies some equality ensuring that $G$ is of cohomological dimension less than two. Groups satisfying this sufficient condition are called mild.If we consider $K$ a number field, then using mild groups, we can construct extensions$L/K$, in which infinitely many primes split completely, and with prescribed Hilbert series Gal(L/K)(t). Consequently Gal(L/K) is finitely generated, infinitely presented and of cohomological dimension $2$.