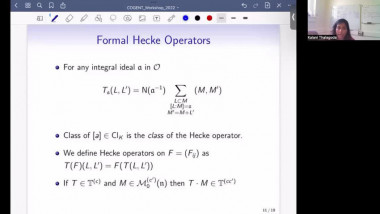
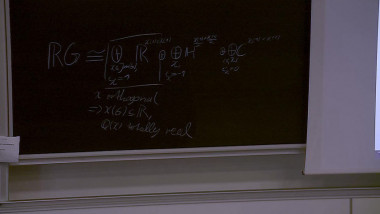Verification of the Quillen conjecture in the rank 2 imaginary quadratic case
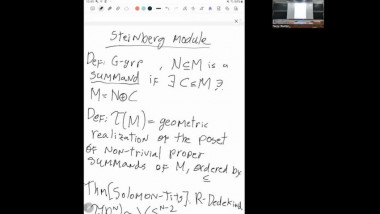
We confirm a conjecture of Quillen in the case of the mod 2 cohomology of arithmetic groups SL(2, A[1/2]), where A is an imaginary quadratic ring of integers. To make explicit the free module structure on the cohomology ring conjectured by Quillen, we compute the mod 2 cohomology of SL(2, B[1/2]) with B the imaginary quadratic ring of discriminant -8 (obtained as the ring of integers from the imaginary quadratic field generated by the square-root of -2) via the amalgamated decomposition of the latter group. This is joint work with Tuan Anh Bui.