Towards reproducibility and transparency in mathematical and computational epidemiology
De Simon Frost
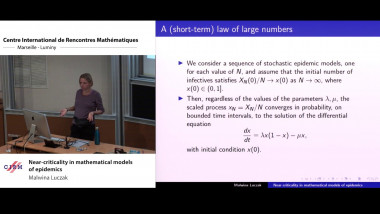
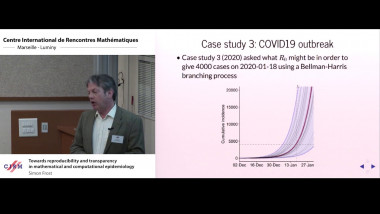
Mathematical models of infectious disease transmission are increasingly used to guide public health and policy decisions. Hence, it is important that every effort is made to ensure that models are ‘correct’, made difficult by the frequent need to simulate a model numerically. The best we can do in most cases is to be able to replicate a model i.e. generate the same results from the same inputs (model plus parameters), or failing that, reproduce results that are similar. This can be achieved by sharing the computer code, and/or providing a sufficiently detailed description of the model. I will illustrate that it is often difficult to replicate or reproduce results of modeling publications, using case studies that highlight some of the many causes of this failure. I will argue that the FAIR principles proposed for data – that they should be Findable, Accessible, Interoperable and Reusable – are equally valid for modeling studies, and go a long way towards ensuring reproducibility. I will present Epirecipes (http://epirecip.es) a FAIR platform that both allows models to be replicated exactly, while fostering the idea that a wide variety of approaches are needed to ensure the robustness of model results. The added value from this platform includes resources for teaching, acting as a ‘Rosetta Stone’ - allowing models from one computer language to be ported to another, and as a repository of best practices, potential pitfalls, and technical tricks that are all too often tucked away in papers or textbooks. As quoted from ‘The Turing Way’ (https://the-turing-way.netlify.com), a handbook for reproducible science, reproducing models of infectious disease should be ‘too easy not to do’.