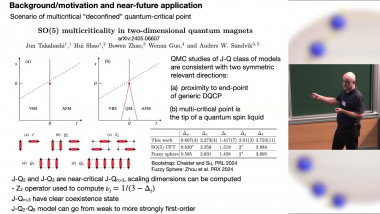
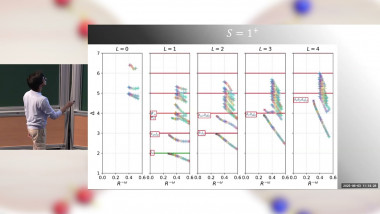
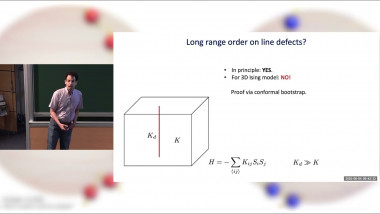
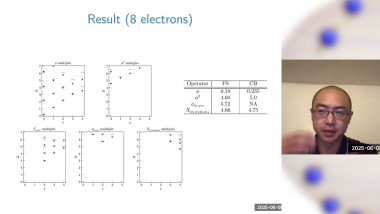
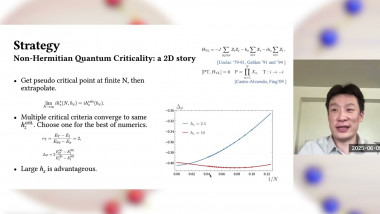
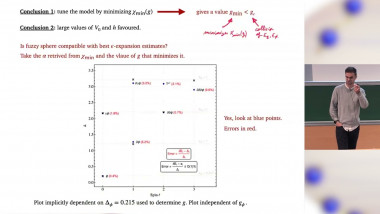
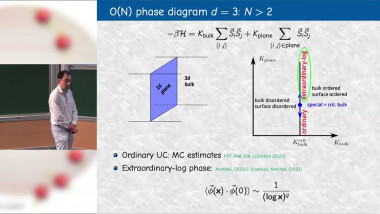
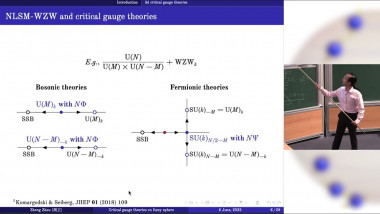
Numerical Simulations of Boundary Critical Phenomena
Recent years have seen a significant advance in our understanding of critical systems in the presence of boundaries and defects. This progress has been driven especially by developments in conformal field theory and in condensed matter physics. In the talk, I review some of these advances, focusing on Monte Carlo studies. In the first part I discuss the boundary critical behavior of the three-dimensional O(N) model, and the physics of the recently discovered extraordinary-log phase. Next, I consider a class of dimerized quantum spin models, whose critical behavior at an edge is not fully understood. In the final part, I present recent Monte Carlo calculations of the boundary operator product expansion of the three-dimensional Ising universality class, for all known surface universality classes.