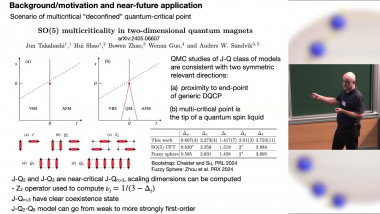
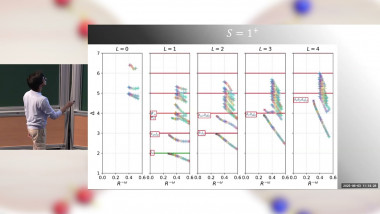
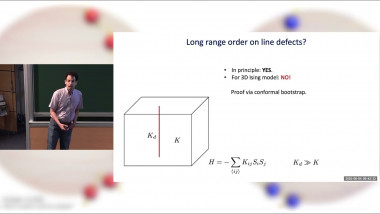
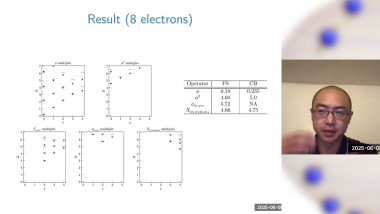
SO(8) unified theory of 2+1 dimensional Dirac fermions and the dark side of the Gross-Neveu model
De Igor Herbut
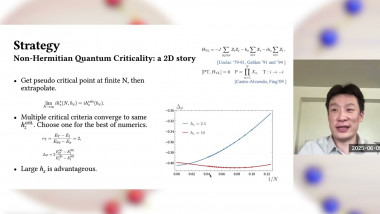
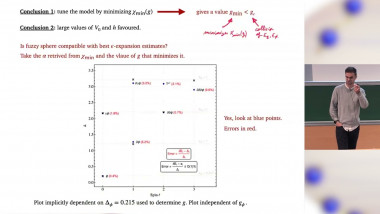
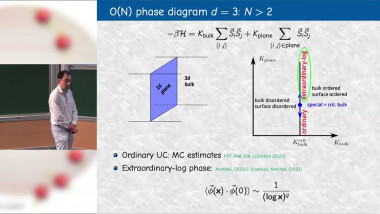
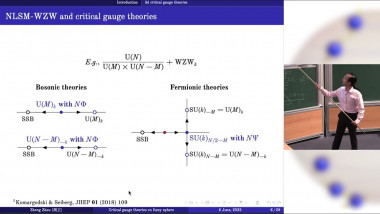
Dirac fermions appear as the low-energy quasiparticle excitations in many condensed matter systems of current interest. They are often weakly interacting, as in graphene for example, but at intermediate interactions they can also exhibit numerous ordered ground states by suffering continuous phase transitions at which gapless fermions play an essential role. I will discuss a unified theory of leading order parameters for Dirac systems in 2+1 dimensions based on their underlying O(8) symmetry. The interacting field theory with the general O(M) symmetry is nothing but the cellebrated Gross-Neveu model. The O(M) symmetry-preserving transition of the Gross-Neveu model for one sign of the interaction coupling is reasonably well understood; I will argue, however, that for the opposite sign of the same coupling the theory could have a previously unsuspected transition at which O(M) spontaneously breaks to O(M/2) x O(M/2). The subtle problem of the universality class of this transition in which the order parameter is a second-rank real tensor coupled to relativistic fermions will be addressed.