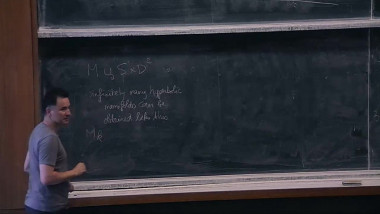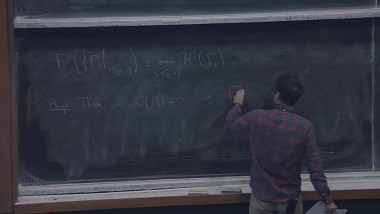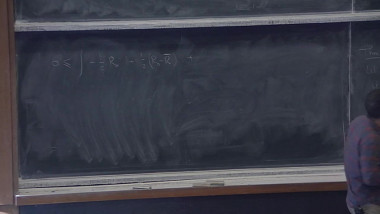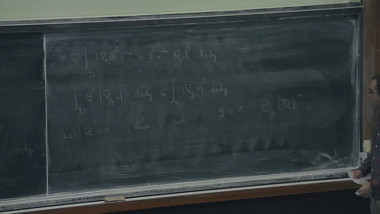The Riemann Mapping Theorem asserts that any simply connected planar domain which is not the whole of it, can be mapped by a conformal homeomorphism onto the open unit disk. After normalization, this map is unique and is called the Riemann mapping. In the 90's, Ken Stephenson, motivated by a circle packing approximation scheme suggested by Thurston (and first proved to converge by Rodin-Sullivan), predicted that the Riemann Mapping may be approximated by a different scheme, i.e., by a sequence of finite networks endowed with particular choices of conductance constants. These networks are naturally defined in terms of the contact graph of any circle packing.We will affirm Stephenson's Conjecture in a greater generality.
By Thomas Richard
By Thomas Richard
By Thomas Richard
By Thomas Richard
By Thomas Richard
By Feng Luo
By Feng Luo
By Feng Luo
By Feng Luo
By Feng Luo
By Feng Luo
By Robert Young
By Buzano Reto
By Ketover Daniel
By Vladimir Markovic
By Melanie Rupflin
By Greg Mcshane
By Jean-Marc Schlenker
By Viaclovsky Jeff
By Wilking Burkhard
