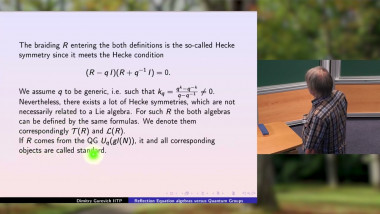
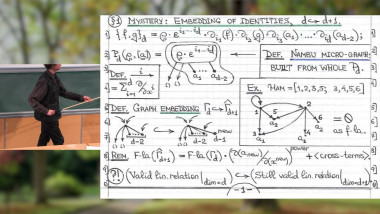
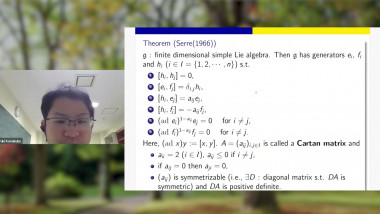
The Weyl algebra (or Heisenberg-Weyl algebra) is the free algebra with two generators $D$ and $U$ and single relation $DU - U D = 1$. As a consequence of this relation, certain monomials are equal, such as $DU U \, D$ and $U \, DDU$. We characterize all such equalities over a field of characteristic 0, describing them in several ways: operational (by a combinatorial equivalence relation generated by certain moves), computational (through lattice path invariants) and in terms of rook theory. We also enumerate the equivalence classes and several variants thereof and discuss possible extensions to other algebras. Joint work with Tom Roby, Stephan Wagner, Mei Yin; inspired by a question of Richard P. Stanley.
By Karol Penson
By Gérard Duchamp
By Jehanne Dousse
By Markus Reineke
By Maxim Kontsevich
By Arthemy Kiselev
By Toshiki Nakashima
By Joseph Ben Geloun
By Stéphane Dartois
By Yuki Kanakubo
By Yiannis Vlassopoulos
By Mohamed Ouerfelli
By Gérard Ben Arous
By Gérard Ben Arous
