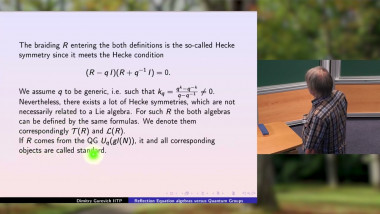
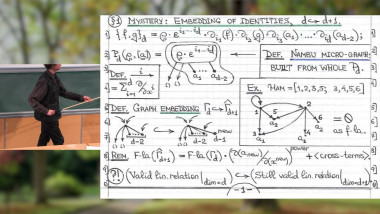
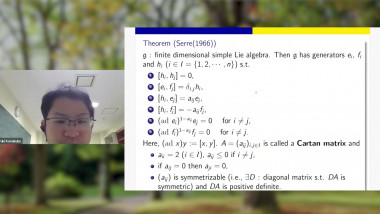
The behavior of multiplicity automata is computable by means of the star of a matrix with noncommutative coefficients taken within a semiring (commutative or noncommutative). Our purpose here is to review applications of this unifying concept (Sweedler's duals, Topological algebras, Infinite iterated integrals). In passing, we indicate how to extend holomorphic-valued shuffle characters as, for example, polylogarithms [1]. In the end of the talk, we will describe a very simple two-state transducer producing the Collatz function. This transducer is the seed of an award-winning recent paper [2]. Work in progress, joint with Didier Caucal (G. Eiffel Lab, Marne-la-Vallée), Nihar Gargava (IRMA, Strasbourg) and Pierre Simonnet (Univ. Corsica). .[1] Gérard H.E. Duchamp, Quoc Huan Ngô and Vincel Hoang Ngoc Minh, Kleene stars of the plane, polylogarithms and symmetries, TCS 800 (2019). .[2] D. Caucal and C. Rispal, On the Powers of the Collatz Function, Best Paper Award of MCU 2024, to be published in LNCS series by Springer Verlag.
By Karol Penson
By Gérard Duchamp
By Jehanne Dousse
By Markus Reineke
By Maxim Kontsevich
By Arthemy Kiselev
By Toshiki Nakashima
By Joseph Ben Geloun
By Stéphane Dartois
By Yuki Kanakubo
By Yiannis Vlassopoulos
By Mohamed Ouerfelli
By Roberta Anna Iseppi
By Alain Connes
