Advancing Bridges in Complex Dynamics / Avancer les connections dans la dynamique complexe

Collection Advancing Bridges in Complex Dynamics / Avancer les connections dans la dynamique complexe

Organizer(s) Benini, Anna Miriam ; Drach, Kostiantyn ; Dudko, Dzmitry ; Hlushchanka, Mikhail ; Schleicher, Dierk

Date(s) 20/09/2021 - 24/09/2021

linked URL https://conferences.cirm-math.fr/2546.html

00:00:00 / 00:00:00

4 27

Quadratic polynomials

By Laurent Bartholdi

Quadratic polynomials have been investigated since the beginnings of complex dynamics, and are often approached through combinatorial theories such as laminations or Hubbard trees. I will explain how both of these approaches fit in a more algebraic framework: that of iterated monodromy groups. The invariant associated with a quadratic polynomial is a group acting on the infinite binary tree, these groups are interesting in their own right, and provide insight and structure to complex dynamics: I will explain in particular how the conversion between Hubbard trees and external angles amounts to a change of basis, how the limbs and wakes may be defined in the language of group theory, and present a model of the Mandelbrot set consisting of groups. This is joint work with Dzmitry Dudko and Volodymyr Nekrashevych.

Information about the video

Date of recording 21/09/2021
Date of publication 02/11/2021
Institution CIRM
Licence CC BY NC ND
Language English
Audience Researchers
Director(s) Guillaume Hennenfent
Format MP4

Citation data

DOI 10.24350/CIRM.V.19810303
Cite this video Bartholdi, Laurent (21/09/2021). Quadratic polynomials. CIRM. Audiovisual resource. DOI: 10.24350/CIRM.V.19810303
URL https://dx.doi.org/10.24350/CIRM.V.19810303

Domain(s)

Bibliography

BARTHOLDI, Laurent et NEKRASHEVYCH, Volodymyr V. Iterated monodromy groups of quadratic polynomials, I. Groups, Geometry, and Dynamics, 2008, vol. 2, no 3, p. 309-336. - https://doi.org/10.4171/GGD/42

MSC codes

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

26:01

published on November 2, 2021

Wandering lakes of Wada

By David Martí-Pete

59:08

published on November 2, 2021

Contracting self-similar groups and conformal dimension

By Volodymyr Nekrashevych

29:23

published on November 2, 2021

Docile transcendental entire functions

By James Waterman

01:01:26

published on November 2, 2021

Quadratic polynomials

By Laurent Bartholdi

01:02:49

published on November 2, 2021

Interbreeding in conformal dynamics, and its applications near and far

By Sabyasachi Mukherjee

01:06:44

published on November 2, 2021

Renormalization in complex dynamics

By Mitsuhiro Shishikura

59:24

published on November 2, 2021

Characterizing Thurston maps by lifting trees

By Rebecca Winarski

01:05:21

published on November 2, 2021

Transcendental functions with small singular sets

By Christopher Bishop

21:59

published on November 2, 2021

Eremenko's conjecture, Devaney's hairs, and the growth of counterexamples

By Andrew Brown

59:25

published on November 2, 2021

Introduction to Thurston's theorems

By John H. Hubbard

27:20

published on November 2, 2021

Entire functions with Cantor bouquet Julia sets

By Leticia Pardo-Simon

32:47

published on November 2, 2021

Hyperbolicity of renormalization for bi-cubic circle maps with bounded combinatorics

By Gabriela Alexandra Estevez Jacinto

35:40

published on November 2, 2021

Transcendental Julia sets of minimal Hausdorff dimension

By Kirill Lazebnik

28:13

published on November 2, 2021

Iterated monodromy groups and transcendental dynamics

By Bernhard Reinke

01:11:08

published on November 2, 2021

Characterizing rational maps positively using graphs

By Dylan Thurston

01:03:26

published on November 2, 2021

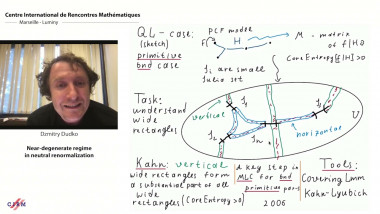
Near-degenerate regime in neutral renormalization

By Dzmitry Dudko

59:41

published on November 2, 2021

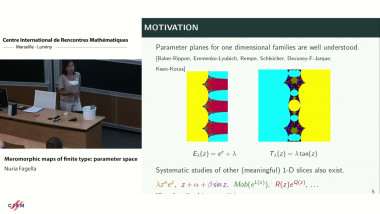
Meromorphic maps of finite type: parameter space

By Nuria Fagella

$A dynamical homeomorphism between the Mandelbrot set $M$ and the parabolic Mandelbrot set $M_{1}$$
58:41

published on November 2, 2021

A dynamical homeomorphism between the Mandelbrot set $M$ and the parabolic Mandelbrot set $M_{1}$

By Carsten Lunde Petersen

33:58

published on November 2, 2021

Transcendental dynamics and infinite-dimensional Thurston theory

By Konstantin Bogdanov

01:06:58

published on November 2, 2021

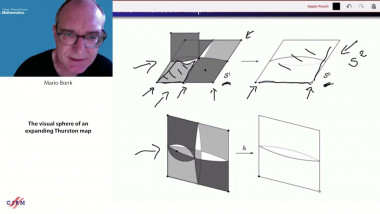
The visual sphere of an expanding Thurston map

By Mario Bonk

01:02:26

published on November 2, 2021

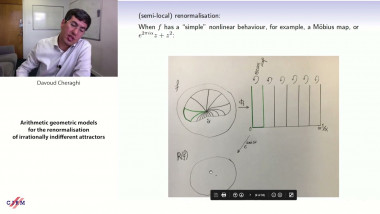
Arithmetic geometric models for the renormalisation of irrationally indifferent attractors

By Davoud Cheraghi

01:04:27

published on November 2, 2021

Box renormalization as a 'black box'

By Kostiantyn Drach

01:13:51

published on November 2, 2021

Story of the Feigenbaum point

By Mikhail Lyubich

32:19

published on November 2, 2021

Transcendental Thurston Theory for entire functions and compositions

By Sergey Shemyakov

01:05:00

published on November 2, 2021

Tips of tongues in the double standard family

By Xavier Buff

54:58

published on November 2, 2021

Decomposition results in rational dynamics

By Mikhail Hlushchanka

54:47

published on November 2, 2021

Polynomial versus transcendental dynamics

By Anna Miriam Benini

Copyright Carmin.tv 2025

Give feedback