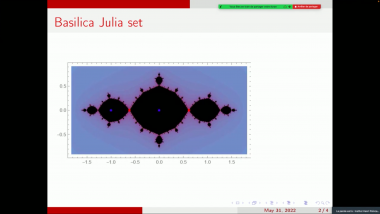
Let $M$ be a metric space and let $T$ be a total ordering of its points. For a finite subset $X\subset M$ we calculate the minimal length $l_{opt}(X)$ of a path visiting all its points, the length $l_T(X)$ of the path which visits the points of $X$ with respect to the order $T$, and the ratio $r_T(X) = l_T(X)/l_{opt}(X)$. As J. Bartholdi and J.Platzman noticed in 1982, for the square $[0;1]^2$ and the order corresponding to the self-similar Peano curve all such ratios $r_T(X)$ are bounded by a logarithmic function of $|X|$. For a given metric space the existence of such "good" orders is connected with more traditional properties and invariants, such as hyperbolicity, Assouad-Nagata dimension, number of ends and doubling. The talk is based on joint works with Anna Erschler.
By Jeremie Brieussel
By Ivan Mitrofanov
By Rostislav Grigorchuk
By Alejandra Garrido
By Dominik Francoeur
By Yair Hartman
By Mikhail Lyubich
By Vadim Kaimanovich
By Anitha Thillaisundaram
By Mikael de la Salle
By Josh Frisch
By Marialaura Noce
By Yves de Cornulier
By Gérard Ben Arous
