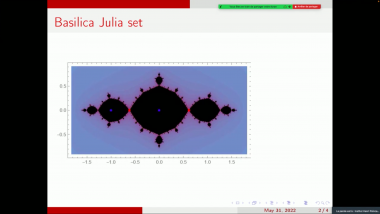
Let $M$ be a metric space and let $T$ be a total ordering of its points. For a finite subset $X\subset M$ we calculate the minimal length $l_{opt}(X)$ of a path visiting all its points, the length $l_T(X)$ of the path which visits the points of $X$ with respect to the order $T$, and the ratio $r_T(X) = l_T(X)/l_{opt}(X)$. As J. Bartholdi and J.Platzman noticed in 1982, for the square $[0;1]^2$ and the order corresponding to the self-similar Peano curve all such ratios $r_T(X)$ are bounded by a logarithmic function of $|X|$. For a given metric space the existence of such "good" orders is connected with more traditional properties and invariants, such as hyperbolicity, Assouad-Nagata dimension, number of ends and doubling. The talk is based on joint works with Anna Erschler.
De Jeremie Brieussel
De Ivan Mitrofanov
De Rostislav Grigorchuk
De Alejandra Garrido
De Dominik Francoeur
De Yair Hartman
De Mikhail Lyubich
De Vadim Kaimanovich
De Anitha Thillaisundaram
De Mikael de la Salle
De Josh Frisch
De Marialaura Noce
De Thomas Ayral
