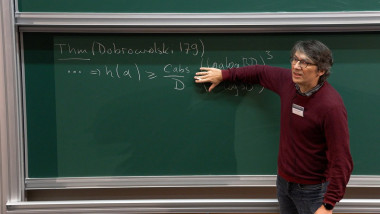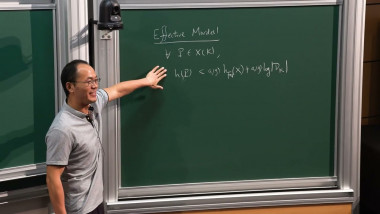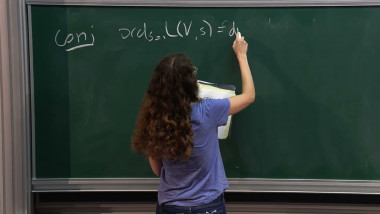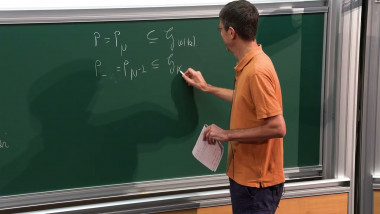Carmin.tv

Mathématiques
et Interactions

Merci de nous donner votre avis pour que nous puissions améliorer votre expérience !
13e Séminaire Itzykson : Bootstrap conforme et géométrie spectrale
3 videos

13e Séminaire Itzykson : Bootstrap conforme et géométrie spectrale

Exposition Laurent Schwartz
4 videos

Exposition Laurent Schwartz

Open science put to the test of rights and duties: mathematicians and librarians, let's educate ours / Science ouverte a l'épreuve des droits et devoirs : mathématiciens-nes et bibliothécaires, (in)formons-nous
8 videos

Open science put to the test of rights and duties: mathematicians and librarians, let's educate ours / Science ouverte a l'épreuve des droits et devoirs : mathématiciens-nes et bibliothécaires, (in)formons-nous

Conférences grand public MathEnVille
1 videos

Conférences grand public MathEnVille

Toutes les collections
CIMPA
CIRM
IHES
IHP
Institut Fourier
LMR
SMF
Tous les instituts
Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Collection Arithmetic and Diophantine Geometry, via Ergodic Theory and o-minimality

Organisateur(s) Ahmed Abbes, Jennifer Balakrishnan, Ziyang Gao, Marc Hindry, Fanny Kassel, Bruno Klingler, Yuri Tschinkel
Date(s) 08/09/2025 - 12/09/2025
URL associée https://indico.math.cnrs.fr/event/13164/
00:00:00 / 00:00:00
14 20

A Quantitative Version of the Uniform Mordell Conjecture

De Xinyi Yuan

The celebrated Mordell conjecture proved by Faltings asserts that the number of rational points on a curve of genus greater than one over a number field is finite. A deep uniform upper bound on the number of rational points follows from Vojta's inequality and the recent works of Dimitrov-Gao-Habegger and Kuhne. In this talk, I will introduce an explicit version of this uniform bound. This is a joint work with Jiawei Yu and Shengxuan Zhou.

Informations sur la vidéo

  • Date de captation 11/09/2025
  • Date de publication 17/09/2025
  • Institut IHES
  • Langue Anglais
  • Audience Chercheurs
  • Format MP4

Domaine(s)

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow




Inscrivez-vous

  • Mettez des vidéos en favori
  • Ajoutez des vidéos à regarder plus tard &
    conservez votre historique de consultation
  • Commentez avec la communauté
    scientifique
  • Recevez des notifications de mise à jour
    de vos sujets favoris
Copyright Carmin.tv 2025
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour améliorer votre expérience. En savoir plus sur notre politique de confidentialité.
Accepter
Donner son avis