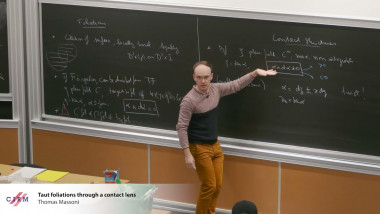Carmin.tv

Mathématiques
et Interactions

Merci de nous donner votre avis pour que nous puissions améliorer votre expérience !
2025 IHES Summer School – Statistical Aspects of Nonlinear Physics
27 videos

2025 IHES Summer School – Statistical Aspects of Nonlinear Physics

AGCT 2025 - Arithmetic, Geometry, Cryptography and Coding Theory / AGCT 2025 - Arithmétique, Géométrie, Cryptographie et Théorie des Codes
6 videos

AGCT 2025 - Arithmetic, Geometry, Cryptography and Coding Theory / AGCT 2025 - Arithmétique, Géométrie, Cryptographie et Théorie des Codes

Perfectly matched perspectives on statistical mechanics, combinatorics and geometry / Perspectives couplées sur la mécanique statistique, la combinatoire et la géométrie
5 videos

Perfectly matched perspectives on statistical mechanics, combinatorics and geometry / Perspectives couplées sur la mécanique statistique, la combinatoire et la géométrie

Fuzzy Sphere Meets Conformal Bootstrap 2025
20 videos

Fuzzy Sphere Meets Conformal Bootstrap 2025

Toutes les collections
CIMPA
CIRM
IHES
IHP
LMR
SMF
Tous les instituts
2021 - T2 - Symplectic topology, contact topology and interactions

Collection 2021 - T2 - Symplectic topology, contact topology and interactions

Organisateur(s) Colin, Vincent ; Humilière, Vincent ; Massot, Patrick ; Niederkrüger, Klaus ; Oancea, Alexandru ; Vaugon, Anne
Date(s) 19/04/2021 - 16/07/2021
URL associée https://indico.math.cnrs.fr/event/5767/
30 45

Persistence K-Theory

De Paul Biran

Apparaît également dans la collection : Giroux 60 - Convexity in contact and symplectic topology

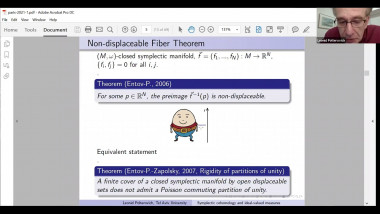
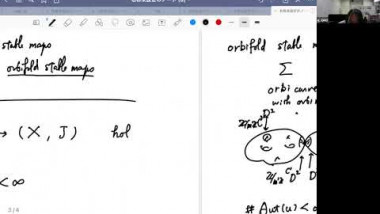
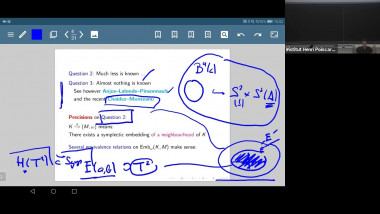
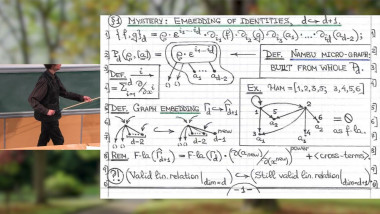
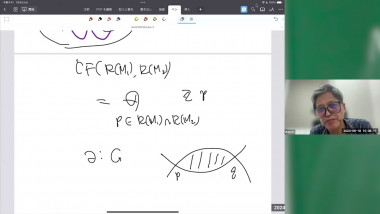
K-theory, in its classical form, associates to a triangulated category an abelian group called the K-group (or the Grothendieck group). Important invariants of various triangulated categories are known to factor through their K-groups. In this talk we will explain the foundations of persistence K-theory, which is an analogous theory for triangulated persistence categories. In particular we will introduce new persistence measurements coming from these K-groups, and new invariants coming from the combination of the persistence and triangulated structures. In the last part of the talk we will exemplify this new theory on the case of the persistence Fukaya category of Lagrangian submanifolds. In particular we will show how our invariants can distinguish between modules that can represent embedded Lagrangians and those who can represent only immersed ones. Based on joint work with Octav Cornea and Jun Zhang.

Informations sur la vidéo

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow




Inscrivez-vous

  • Mettez des vidéos en favori
  • Ajoutez des vidéos à regarder plus tard &
    conservez votre historique de consultation
  • Commentez avec la communauté
    scientifique
  • Recevez des notifications de mise à jour
    de vos sujets favoris
Copyright Carmin.tv 2025
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour améliorer votre expérience. En savoir plus sur notre politique de confidentialité.
Accepter
Donner son avis