Appears in collection : Slava Rychkov – Random Field Ising Model and Parisi-Sourlas Supersymmetry
Numerical evidence suggests that the Random Field Ising Model loses Parisi-Sourlas SUSY and the dimensional reduction property somewhere between 4 and 5 dimensions, while a related model of branched polymers retains these features in any d. I will present a recent theory, developed in 2019-2021 jointly with A. Kaviraj and E. Trevisani and published in [1-4], which aims to explain these facts.
Outline:
- Random Field Ising Model: phase diagram, well-established facts and experiments.
- Numerical results for the dimensional reduction of critical exponents: “no” for d=3,4, “yes” for d=5.
- Parisi-Sourlas supersymmetry implies dimensional reduction
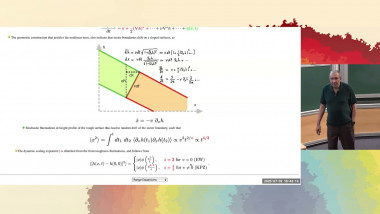
- Generalities about RG fixed point disappearance
- Loss of Parisi-Sourlas SUSY via dangerously irrelevant operators?
- Replica field theory. Cardy field transform “derivation" of Parisi-Sourlas SUSY and its potential loopholes.
- Replica symmetric interactions in the Cardy basis
- Leader and follower interactions
- Classification of leaders
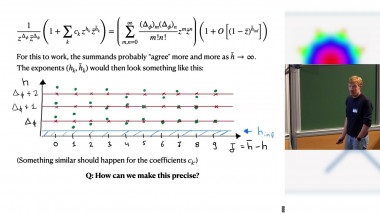
- Anomalous dimension computations and results. Evidence for the SUSY fixed point instability below ~4.5
- Future directions and open problems.