
Isomonodromic deformations, exact WKB analysis and Painlevé 1
By Olivier Marchal
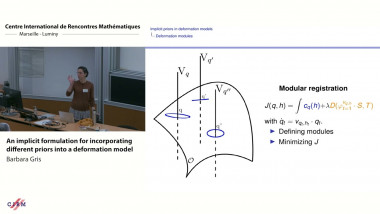
An implicit formulation for incorporating different priors into a deformation model
By Barbara Gris

Integration on Grassmannians and deformed monotone Hurwitz numbers
By Norman Do

Topological Recursion, Painlevé Equation, Exact WKB and Resurgence
By Kohei Iwaki











