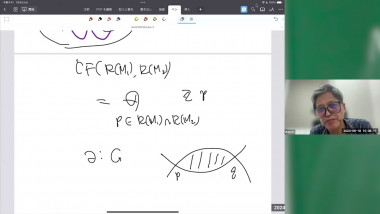
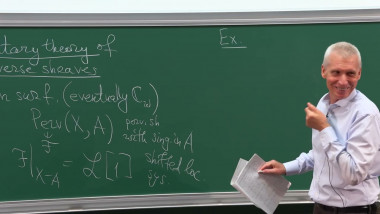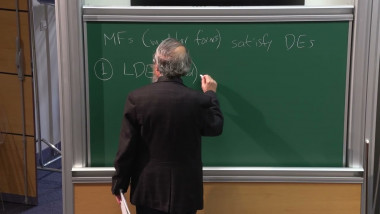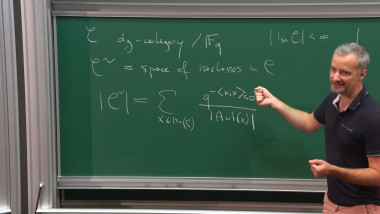Shimurian analogs of Barsotti-Tate groups.
I will first recall Grothendieck's notion of n-truncated Barsotti-Tate group. Such groups form an algebraic stack over the integers. The problem is to give an illuminating description of its reductions modulo powers of p. A related problem is to construct analogs of these reductions related to general Shimura varieties with good reduction at p. Some time ago I formulated conjectures which address these problems. The conjectures have been proved by Z.Gardner, K.Madapusi, and A.Mathew. In particular, they developed a modern version of Dieudonné theory.