Semialgebraic Whitney partition of unity
By Anna Valette
This talk is based on a common work with Wieslaw Pawlucki and Beata Kocel-Cynk. I will present a notion of $\mathrm{\wedge }_{p}$-regular partition of unity which can be seen as a semialgebraic counterpart of Whitney partition of unity. This enables us to obtain a semialgebraic (or more generally definable) version of Calder´on Zygmund theorem on regularization of the distance function. Some more consequences will also be given.












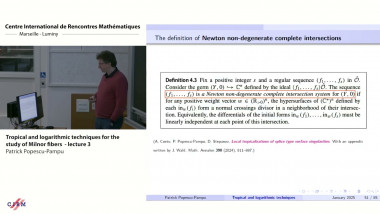





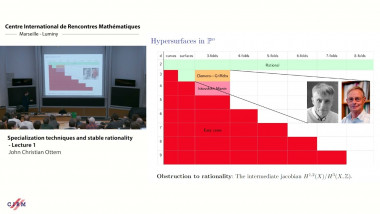

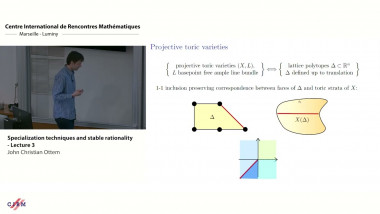
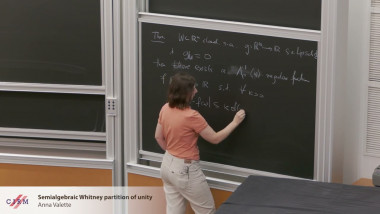










![[1245] Model theory, differential algebra and functional transcendence](/media/cache/video_light/uploads/video/SeminaireBourbaki.jpg)




