Jean Morlet Chair - 2020 - Sem 2 - Tichy - Rivat

Collection Jean Morlet Chair - 2020 - Sem 2 - Tichy - Rivat

Organizer(s) Prof. Robert TICHY Technische Universität Graz and Prof. Joël RIVAT Aix-Marseille Université

Date(s) 01/09/2020 - 28/09/2021

linked URL https://www.chairejeanmorlet.com/2020-2-tichy-rivat.html

00:00:00 / 00:00:00

23 56

Fibonacci numbers and repdigits

By Florian Luca

Also appears in collection : Jean-Morlet Chair 2020 - Conference: Diophantine Problems, Determinism and Randomness / Chaire Jean-Morlet 2020 - Conférence : Problèmes diophantiens, déterminisme et aléatoire

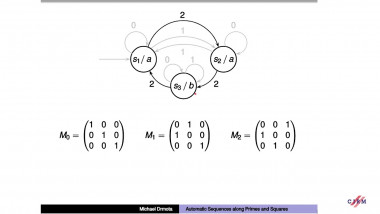
In the first part of the talk we will survey known results concerning Fibonacci numbers whose digital representations in base 10 display some interesting patterns. In the second part of the talk we will give the main steps of the proof of a recent result which states that $b = 4$ is the only integer ≥ 2 such that there are two Fibonacci numbers larger than 1 which are repunits in base b. In this case, $F_{5}=(4^{2}-1)/(4-1)$ and $F_{8}=(4^{3}-1)/(4-1)$. This is joint work with C. A. Gomez and J. C. Gomez from Cali, Colombia.

Information about the video

Date of recording 26/11/2020
Date of publication 01/12/2020
Institution CIRM
Licence CC BY NC ND
Language English
Audience Researchers
Director(s) Guillaume Hennenfent
Format MP4

Citation data

DOI 10.24350/CIRM.V.19687803
Cite this video Luca, Florian (26/11/2020). Fibonacci numbers and repdigits. CIRM. Audiovisual resource. DOI: 10.24350/CIRM.V.19687803
URL https://dx.doi.org/10.24350/CIRM.V.19687803

Domain(s)

Number Theory

Bibliography

Luca, F. Fibonacci and Lucas numbers with only one distinct digit. Portugal. Math. 57 (2000), no. 2, 243-254. - https://www.emis.de/journals/PM/57f2/pm57f209.pdf
Bravo, Jhon J.; Luca, Florian On a conjecture about repdigits in k-generalized Fibonacci sequences. Publ. Math. Debrecen 82 (2013), no. 3-4, 623-639. -

MSC codes

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

15 videos

published on July 28, 2022

Jean-Morlet Chair 2020 - Research School: Quasi-Monte Carlo Methods and Applications / Chaire Jean-Morlet 2020 - Ecole: Méthode de quasi-Monte-Carlo et applications

28 videos

published on July 11, 2022

Jean-Morlet Chair 2020 - Conference: Diophantine Problems, Determinism and Randomness / Chaire Jean-Morlet 2020 - Conférence : Problèmes diophantiens, déterminisme et aléatoire

3 videos

published on July 29, 2022

Jean-Morlet Chair 2020 (2) - Workshop: Discrepancy Theory and Applications - Part 2 / Chaire Jean-Morlet 2020 (2) - Workshop : Théorie de la discrépance et applications - Part 2

9 videos

published on July 11, 2022

Jean-Morlet Chair 2020 - Workshop: Discrepancy Theory and Applications - Part 1 / Chaire Jean-Morlet 2020 - Workshop : Théorie de la discrépance et applications - Part 1

17:54

published on February 24, 2021

Interview at Cirm : Robert Tichy

By Robert Tichy

Copyright Carmin.tv 2025

Give feedback