An integration approach to the Toeplitz square peg problem
By Terence Tao
Also appears in collections : Harmonic analysis and geometric measure theory / Analyse harmonique et théorie géométrique de la mesure, The Fields Medallists
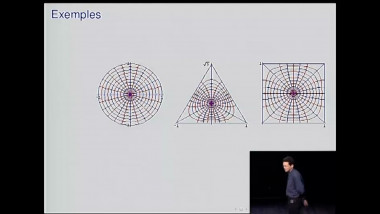
The Toeplitz square peg problem asks if every simple closed curve in the plane inscribes a square. This is known for sufficiently regular curves (e.g. polygons), but is open in general. We show that the answer is affirmative if the curve consists of two Lipschitz graphs of constant less than 1 using an integration by parts technique, and give some related problems which look more tractable.