Schatten Properties of Commutators
By Kai Zeng
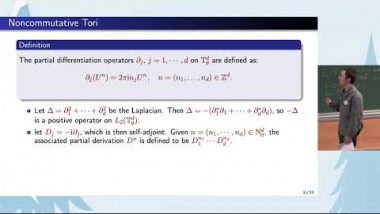
Given a quantum tori $\mathbb{T}_{\theta}^d$, we can define the Riesz transforms $\mathfrak{R}_j$ on the quantum tori and the commutator $đx_i$ := [$\mathfrak{R}_i,M_x$], where $M_x$ is the operator on $L^2(\mathbb{T}_{\theta}^d)$ of pointwise multiplication by $x \in L^\infty (\mathbb{T}_{\theta}^d)$. In this talk, we will characterize the Schatten properties of the commutator [$\mathfrak{R}_i,M_x$] by showing that $x \in B_{p,q}^{\alpha} ({\mathbb T}_{\theta}^d)$, where $B_{p,q}^{\alpha} ({\mathbb T}_{\theta}^d)$ is the Besov space on quantum tori. Futhermore, we will extend this characterisation to the more general case where $\mathfrak{R}_j$ replaced by an arbitrary Calderon-Zygmund operator. To date, these new results treat the quantum differentiability in the strictly noncommutative setting.