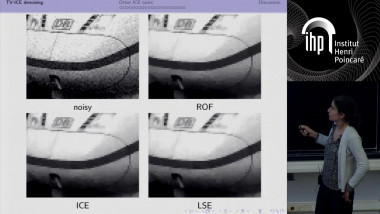
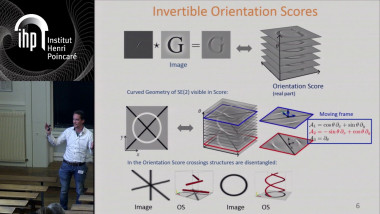
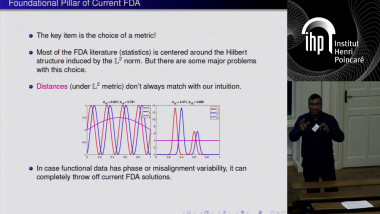
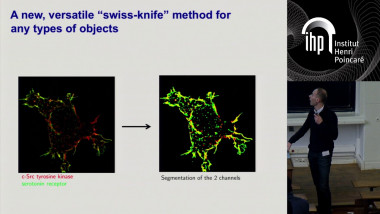
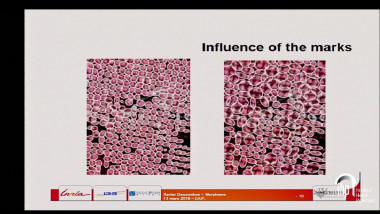
Total variation denoising with iterated conditional expectation
Imaging tasks most often require an energy minimization interpretable in a probabilistic approach as a maximum a posteriori. Taking instead the expectation a posteriori gives an interesting alternative but confronts the question of numerical integration in high dimension. We propose a variable-at-a-time integration, called after by iterated conditional expectation (ICE), that approximates the expectation a posteriori. We try it on total variation denoising for which it gives good visual properties and linear convergence. We give several clues concerning extensions of the method. Joint work with Lionel Moisan.