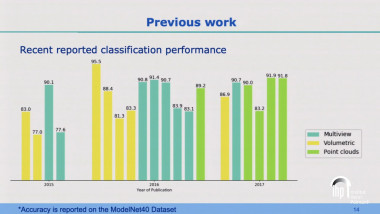
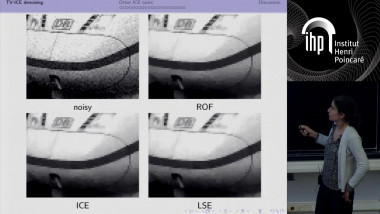
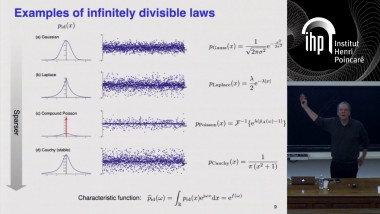
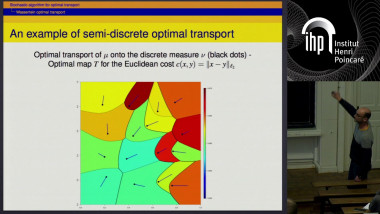
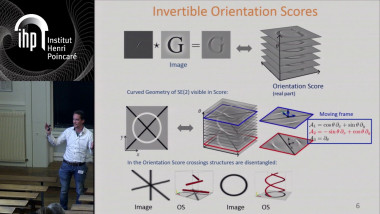
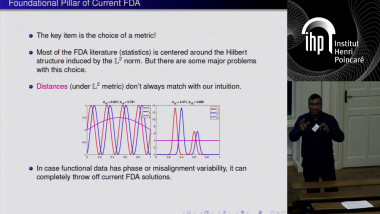
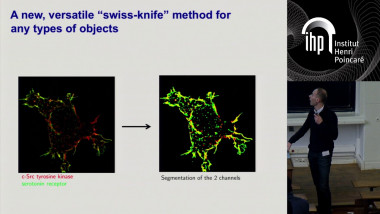
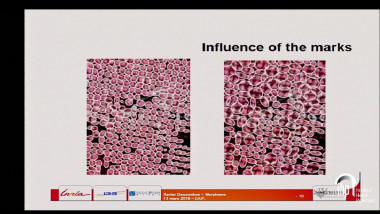
Hybrid sparse stochastic processes and the resolution of linear inverse problems
Sparse stochastic processes are continuous-domain processes that are specified as solutions of linear stochastic differential equations driven by white Lévy noise. These processes admit a parsimonious representation in some matched wavelet-like basis. Such models are relevant for image compression, compressed sensing, and, more generally, for the derivation of statistical algorithms for solving ill-posed inverse problems. The hybrid processes of this talk are formed by taking a sum of such elementary processes plus an optional Gaussian component. We apply this hybrid model to the derivation of image reconstruction algorithms from noisy linear measurements. In particular, we derive a hybrid MAP estimator, which is able to successfully reconstruct signals, while identifying the underlying signal components. Our scheme is compatible with classical Tikhonov and total-variation regularization, which are both recovered as limit cases. We present an efficient ADMM implementation and illustrate the advantages of the hybrid model with concrete examples.