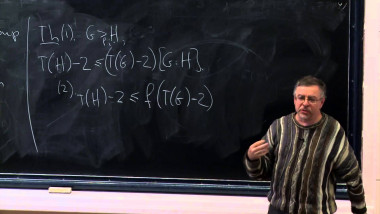Also appears in collection : Fields medallists - 2010
In contrast to the two dimensional case, in dimension $d \geq 3$ averaging operators on the $d-1$-sphere using finitely many rotations, i.e. averaging operators of the form $Af(x)= |S|^{-1} \sum_{\theta \in S} f(s x)$ where $S$ is a finite subset of $SO (d)$, can have a spectral gap on $L^2$ of the $d-1$-sphere. A result of Bourgain and Gamburd shows that this holds, for instance, for any finite set of elements in $\SO (3)$ with algebraic entries and spanning a dense subgroup. We prove a new spectral gap result for averaging operators corresponding to finite subsets of the isometry group of $R^d$, which is a semi-direct product of $SO (d)$ and $R^d$, provided the averaging operator corresponding to the rotation part of these elements have a spectral gap. This new spectral gap result has several applications, in particular to the study of self similar measures in $d \geq 3$ dimensions, and can be used to give sharpening to a previous result of Varju regarding random walks on $R^d$ using the elements of the isometry group. Joint work with Peter Varju
