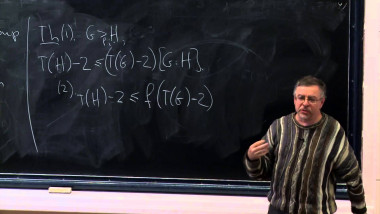2014 - T1 - WS1 - Asymptotic properties of groups

Collection 2014 - T1 - WS1 - Asymptotic properties of groups

Organizer(s) Breuillard, Emmanuel ; Chatterji, Indira ; Erschler, Anna

Date(s) 24/03/2014 - 28/03/2014

linked URL https://web.archive.org/web/20220123001204/https://sites.google.com/site/geowalks2014/home/workshop

00:00:00 / 00:00:00

16 21

Relative growth of subgroups in finitely generated groups

By Alexander Olshanskii

Let $H$ be a subgroup of a finitely generated group $G$. The (relative) growth function $f(n)$ of $H$ with respect to a finite set $A$ generating $G$, is given by the formula $f(n) = card \{g\in H; |g|_A \le n}$. I want to review some recent results on the asymptotic behavior of relative growth functions in free, solvable and other groups.

Information about the video

Date of publication 14/04/2014
Institution IHP
Licence CC BY-NC-ND
Format MP4

Domain(s)

Group Theory

MSC codes

Last related questions on MathOverflow

You have to connect your Carmin.tv account with mathoverflow to add question

Ask a question on MathOverflow

All the collection videos

41:54

published on April 14, 2014

Invariant random subgroups of groups of the lamplighter type

By Rostislav Grigorchuk

47:00

published on April 14, 2014

Quantum error correcting codes and asymptotic properties of 4-dimensional arithmetic hyperbolic manifolds

By Alex Lubotzky

53:51

published on April 14, 2014

On best possible rates of Diophantine approximation by lattice orbits.

By Amos Nevo

50:18

published on April 14, 2014

Spectral gap, random walks on Euclidean isometry groups, and self-similar measures.

By Elon Lindenstrauss

49:58

published on April 14, 2014

Free Engel Groups and Similar Groups

By Elyahu Rips

48:48

published on April 14, 2014

Sheaves on Graphs, L^2 Betti Numbers, and Applications.

By Joel Friedman

43:44

published on April 14, 2014

Metric ultraproducts of finite simple groups

By John Wilson

50:38

published on April 14, 2014

Imbeddings in groups of subexponential growth

By Laurent Bartholdi

50:40

published on April 14, 2014

The Tarski numbers of groups.

By Mark Sapir

50:50

published on April 14, 2014

Profinite isomorphism problems.

By Martin Bridson

49:41

published on April 14, 2014

Invariant random subgroups.

By Miklos Abert

47:40

published on April 14, 2014

On the asymptotic dimension of a curve complex.

By Mladen Bestvina

46:50

published on April 14, 2014

Cutting and pasting: a group for Frankenstein

By Nicolas Monod

49:26

published on April 14, 2014

Right angled cocompact lattices in higher rank simple Lie groups.

By Nikolay Nikolov

40:37

published on April 14, 2014

Holomorphic families of Riemann surfaces from the point of view of asymptotic group theory

By Thomas Delzant

44:13

published on April 14, 2014

Relative growth of subgroups in finitely generated groups

By Alexander Olshanskii

47:16

published on April 14, 2014

Outer space for right-angled Artin groups

By Karen Vogtmann

48:06

published on April 14, 2014

Similar Relatively hyperbolic actions of a group

By Leonid Potyagailo

50:35

published on April 14, 2014

Random walk on p-adic flag varieties

By Yves Benoist

46:50

published on April 14, 2014

Envelopes and equivalence relations in a free group

By Zlil Sela

48:30

published on April 14, 2014

Vertex finiteness for relatively hyperbolic groups

By Gilbert Levitt

Copyright Carmin.tv 2025

Give feedback