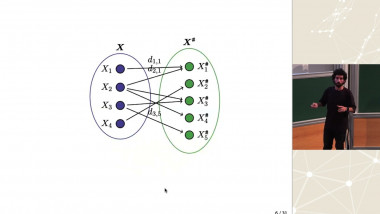
In this talk, we consider the problem of estimating the matching map between two sequences of $d$-dimensional noisy observations of feature vectors, possibly of different sizes ($n \neq m$). We begin with the simplest case of permutation estimation and then extend it to the more general setting of estimating a matching map of unknown size $k^* < \min(n, m)$. Our main result shows that, in the high-dimensional setting, if the signal-to-noise ratio of the feature vectors is at least of order $d^{1/4}$, then the true matching map can be recovered exactly (without errors) with high probability. We also establish a corresponding lower bound, proving the optimality of this rate. This rate is achieved using an estimated matching, defined as the minimizer of the sum of squared distances between matched pairs of points. Since the number of matching pairs is unknown, we first estimate the parameter $k^_$. We then show that the resulting optimization problem can be formulated as a minimum-cost flow problem and solved efficiently, with complexity $\widetilde{O}(\sqrt{k^_} n^2)$. Finally, we present numerical experiments on both synthetic and real-world data, illustrating our theoretical results and providing further insight into the properties of the estimators and algorithms studied in this work. \textit{Joint work with T. Galstyan, S. Hunanyan, and A. Dalalyan.}