1/3 Algebraic K-theory and Trace Methods
Apparaît également dans la collection : Teena Gerhardt - Algebraic K-theory and Trace Methods
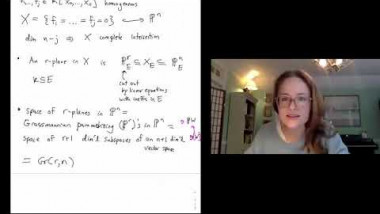
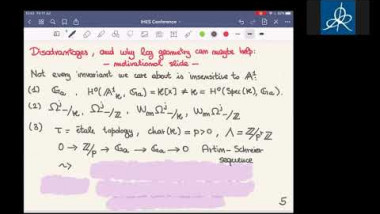
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approach to studying algebraic K-theory is via trace maps, relating algebraic K-theory to (topological) Hochschild homology, and (topological) cyclic homology. In this mini-course I will introduce algebraic K-theory and related Hochschild invariants, and discuss recent advances in this area. Topics will include cyclotomic spectra, computations of the algebraic K-theory of rings, and equivariant analogues of Hochschild invariants.