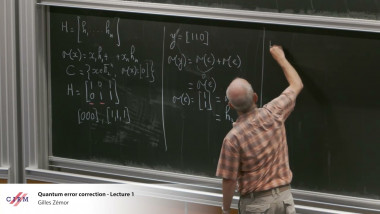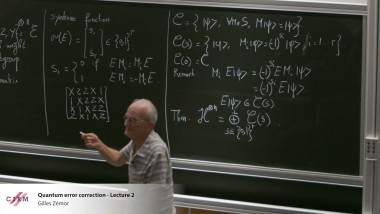Carmin.tv

Mathématiques
et Interactions

Merci de nous donner votre avis pour que nous puissions améliorer votre expérience !
Not Only Scalar Curvature Seminar
74 videos

Not Only Scalar Curvature Seminar

Geometric structures and discrete group actions / Structures géométriques et actions de groupes discrets
4 videos

Geometric structures and discrete group actions / Structures géométriques et actions de groupes discrets

Misha Gromov : Mathematical Description of Biological Structures
4 videos

Misha Gromov : Mathematical Description of Biological Structures

Applications of NonCommutative Geometry to Gauge Theories, Field Theories, and Quantum Space-Time / Applications de la Géométrie Non Commutative aux Théories de Jauge, à la Théorie des Champs et aux Espaces-Temps Quantiques
5 videos

Applications of NonCommutative Geometry to Gauge Theories, Field Theories, and Quantum Space-Time / Applications de la Géométrie Non Commutative aux Théories de Jauge, à la Théorie des Champs et aux Espaces-Temps Quantiques

Toutes les collections
CIMPA
CIRM
IHES
IHP
LMR
SMF
Tous les instituts
2024 - T3 - WS2 - Emerging topics in design and cryptanalysis of post-quantum schemes

Collection 2024 - T3 - WS2 - Emerging topics in design and cryptanalysis of post-quantum schemes

Organisateur(s) Chakraborty, Olive ; Kahrobaei, Delaram ; Perret, Ludovic ; Robinson, Angela
Date(s) 04/11/2024 - 08/11/2024
URL associée https://indico.math.cnrs.fr/event/5777/
11 20

Improved Attacks for SNOVA by Exploiting Stability under a Group Action

De Javier Verbel

SNOVA is a post-quantum digital signature scheme based on multivariate polynomials, that stands out in the ongoing NIST competition for its efficiency and compactness. Recently, there have been several attacks that reduce to solving a structured system of quadratic polynomials. In this talk, I discuss a recent work in which we propose a polynomial solving algorithm tailored for SNOVA systems, which exploits the stability of the system under the action of a commutative group of matrices, to reduce the complexity to solve SNOVA systems. We show how to adapt the reconciliation and direct attacks in order to profit from this new algorithm. Consequently, we improve the reconciliation attack for all SNOVA parameter sets with speedup factors ranging between 2^3 and 2^{22}. Our algorithm also reduces the complexity of the direct attack for several parameter sets. It is particularly effective for the parameters that give the best performance to SNOVA $(l=4)$, and brings these parameter sets below NIST's security threshold with speedup factors between 2^{33} and 2^{52}, over the state-of-the-art.

Informations sur la vidéo

Données de citation

  • DOI 10.57987/IHP.2024.T3.WS2.011
  • Citer cette vidéo Verbel, Javier (06/11/2024). Improved Attacks for SNOVA by Exploiting Stability under a Group Action. IHP. Audiovisual resource. DOI: 10.57987/IHP.2024.T3.WS2.011
  • URL https://dx.doi.org/10.57987/IHP.2024.T3.WS2.011

Domaine(s)

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow




Inscrivez-vous

  • Mettez des vidéos en favori
  • Ajoutez des vidéos à regarder plus tard &
    conservez votre historique de consultation
  • Commentez avec la communauté
    scientifique
  • Recevez des notifications de mise à jour
    de vos sujets favoris
Copyright Carmin.tv 2025
En poursuivant votre navigation sur ce site, vous acceptez l'utilisation de cookies pour améliorer votre expérience. En savoir plus sur notre politique de confidentialité.
Accepter
Donner son avis