Collection 2021 - T2 - Symplectic topology, contact topology and interactions

Organisateur(s) Colin, Vincent ; Humilière, Vincent ; Massot, Patrick ; Niederkrüger, Klaus ; Oancea, Alexandru ; Vaugon, Anne

Date(s) 19/04/2021 - 16/07/2021

URL associée https://indico.math.cnrs.fr/event/5767/

25 45

SFT-Style Rabinowitz complex for exact Lagrangian cobordisms and Calabi-Yau isomorphisms

De Noémie Legout

Apparaît également dans la collection : Giroux 60 - Convexity in contact and symplectic topology

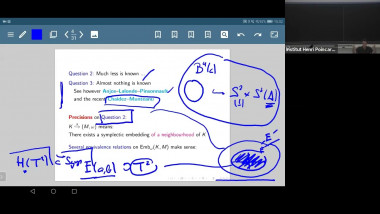
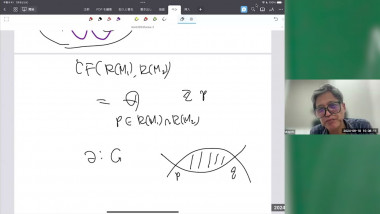
We will define a Floer complex (the "Rabinowitz" complex) associated to a pair of exact Lagrangian cobordisms, using SFT techniques. This complex is a DG-bimodule over the Chekanov-Eliashberg algebras of the Legendrian submanifolds in the negative end of the cobordisms. We will use this complex and its properties to show that the Chekanov-Eliashberg algebra of an horizontally displaceable Legendrian sphere satisfies some Calabi-Yau property, namely that it is quasi-isomorphic as a DG-bimodule over itself to its inverse dualizing bimodule.

Informations sur la vidéo

Date de captation 07/07/2022
Date de publication 07/07/2025
Institut IHP
Licence CC BY-NC-ND
Langue Anglais
Audience Chercheurs
Réalisateur(s) Marco Perez
Format MP4
Lieu IHP - Hermite Amphitheater

Dernières questions liées sur MathOverflow

Pour poser une question, votre compte Carmin.tv doit être connecté à mathoverflow

Poser une question sur MathOverflow

Toutes les vidéos de la collection

06:00

publiée le 16 juillet 2021

Presentation of the T2 2021 : "Symplectic topology, contact topology and interactions"

5 videos

publiée le 23 mai 2022

From Hamiltonian Dynamics to Symplectic Topology

8 videos

publiée le 21 mai 2021

2021 - T2 - WS2 - Advances in symplectic topology

18 videos

publiée le 8 août 2022

Giroux 60 - Convexity in contact and symplectic topology

01:08:16

publiée le 7 mai 2021

Many real projective spaces are not Liouville fillable

De Paolo Ghiggini

01:05:53

publiée le 7 mai 2021

Compact objects in the Fukaya category and representations of Eliashberg-Chekanov algebra

De Baptiste Chantraine

01:07:11

publiée le 28 mai 2021

A few properties of Besse contact manifolds.

De Marco Mazzucchelli

01:05:53

publiée le 11 juin 2021

The genus-one question for open book decomposition

De Pierre Dehornoy

59:28

publiée le 18 juin 2021

Khovanov homology and the cinquefoil

De Steven Sivek

01:03:00

publiée le 18 juin 2021

Tropical Fukaya Algebras

De Sushmita Venugopalan

01:13:35

publiée le 18 juin 2021

Rabinowitz Floer complex for Lagrangian cobordisms

De Noémie Legout

01:00:53

publiée le 2 juillet 2021

Symplectic cohomology and ideal valued measures

De Leonid Polterovich

01:15:38

publiée le 2 juillet 2021

String topology and self-intersections

De Nancy Hingston

01:27:49

publiée le 2 juillet 2021

Non-squeezing of Legendrian knots into neighbourhoods of non-Legendrians and C^0 contactomorphisms

De Georgios Dimitroglou Rizell

01:20:27

publiée le 2 juillet 2021

Orbifold Lagrangian Floer theory

De Kaoru Ono

59:12

publiée le 13 juillet 2021

Progress towards new examples of knot-filtered ECH

De Morgan Weiler

01:17:24

publiée le 2 juillet 2021

Symplectically knotted cubes

De Felix Schlenk

Mathématiques
et Interactions

2025 IHES Summer School – Discrete Subgroups of Lie Groups : Dynamics, Actions, Rigidity

2025 IHES Summer School – Statistical Aspects of Nonlinear Physics

AGCT 2025 - Arithmetic, Geometry, Cryptography and Coding Theory / AGCT 2025 - Arithmétique, Géométrie, Cryptographie et Théorie des Codes

Perfectly matched perspectives on statistical mechanics, combinatorics and geometry / Perspectives couplées sur la mécanique statistique, la combinatoire et la géométrie

Collection 2021 - T2 - Symplectic topology, contact topology and interactions

SFT-Style Rabinowitz complex for exact Lagrangian cobordisms and Calabi-Yau isomorphisms

Informations sur la vidéo

Dernières questions liées sur MathOverflow

Poser une question sur MathOverflow

Presentation of the T2 2021 : "Symplectic topology, contact topology and interactions"

From Hamiltonian Dynamics to Symplectic Topology

2021 - T2 - WS2 - Advances in symplectic topology

Giroux 60 - Convexity in contact and symplectic topology

Many real projective spaces are not Liouville fillable

Compact objects in the Fukaya category and representations of Eliashberg-Chekanov algebra

A few properties of Besse contact manifolds.

The genus-one question for open book decomposition

Khovanov homology and the cinquefoil

Tropical Fukaya Algebras

Rabinowitz Floer complex for Lagrangian cobordisms

Symplectic cohomology and ideal valued measures

String topology and self-intersections

Non-squeezing of Legendrian knots into neighbourhoods of non-Legendrians and C^0 contactomorphisms

Orbifold Lagrangian Floer theory

Progress towards new examples of knot-filtered ECH

Symplectically knotted cubes

Taut foliations through a contact lens

Recent progress on groups of area-preserving homeomorphisms

New identities for differential-polynomial structures built from Jacobian determinants

$A$ Infinity Functor in Symplectic Geometry and Gauge Theory

An Update on SYZ Mirror Symmetry and Family Floer Theory

SFT-Style Rabinowitz complex for exact Lagrangian cobordisms and Calabi-Yau isomorphisms

Informations sur la vidéo

Dernières questions liées sur MathOverflow

Poser une question sur MathOverflow

Inscrivez-vous