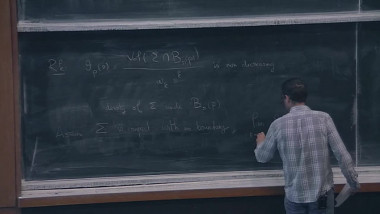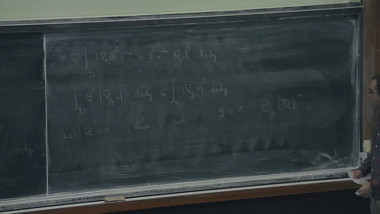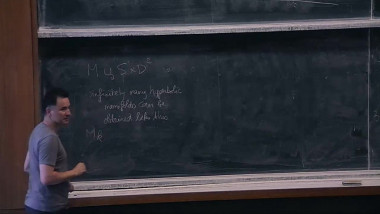Schlenker and Krasnov have established a remarkable Schlaffli-type formula for the (renormalized) volume of a quasi-Fuchsian manifold. Using this, some classical results in complex analysis and Gromov-Hausdorff convergence for sequences of open 3-manifolds due to Brock-Bromberg one obtains explicit upper bounds for the volume of a mapping torus in terms of the translation distance of the monodromy on Teichmueller space. We will explain Brock-Bromberg's approach to the Thurston's uniformization theorem for hyperbolic manifolds which are mapping tori. In particular the "coarse geometry" of the convex core of a quasi fuchsian manifold.