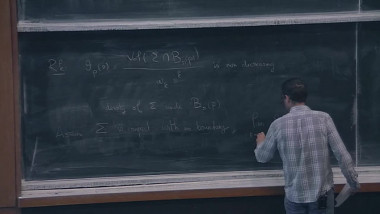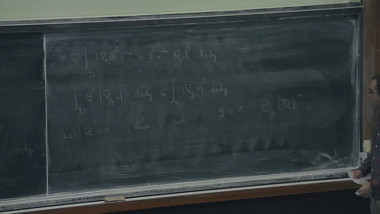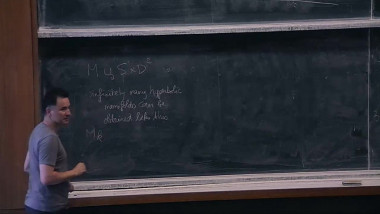(joint work with Assaf Naor) The Heisenberg group $\mathbb{H}$ is a sub-Riemannian manifold that is unusually difficult to embed in $\mathbb{R}^n$. Cheeger and Kleiner introduced a new notion of differentiation that they used to show that it does not embed nicely into $L_1$. This notion is based on surfaces in $\mathbb{H}$, and in this talk, we will describe new techniques that let us quantify the "roughness" of such surfaces, find sharp bounds on the distortion of embeddings of $\mathbb{H}$, and estimate the accuracy of an approximate algorithm for the Sparsest Cut Problem.