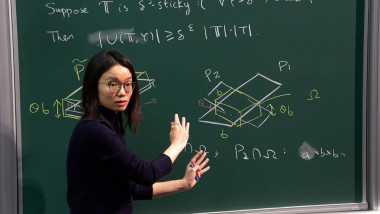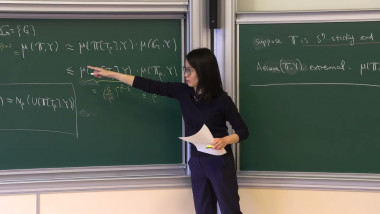Appears in collection : New perspectives on Borel summation

The second day’s lectures are dedicated to a family of examples: the Airy-Lucas functions introduced by Charbonnier et al. (arXiv:2203.16523). These functions satisfy linear ODEs that generalize the Airy equation. They can also, like the Airy function, be expressed as thimble integrals. We will explain, from both perspectives, why these solutions can be obtained by Borel summation. We first discuss the linear ODE perspective, with the help of our work in progress on integral equations (arXiv:2309.00603).

Joint work with Veronica Fantini.

References:

(3:59) https://arxiv.org/abs/2203.16523

(33:25) https://arxiv.org/abs/2309.00603

Corrections:

(3:59) Name should be spelled Charbonnier

(44:42) Parameters should be ₂F₁(1/2 − m/n, 1/2 + m/n, 1/2, ...)