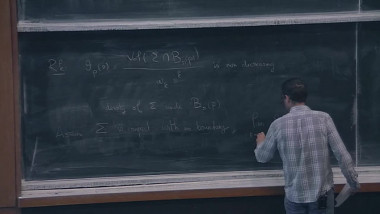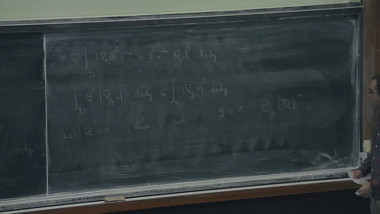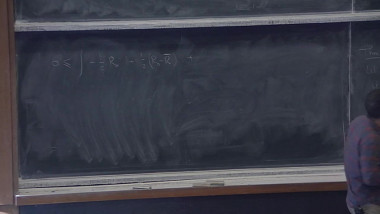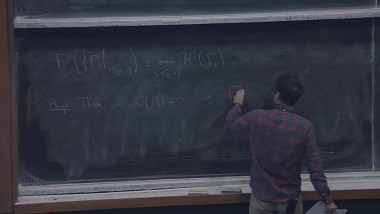The goal of these lectures is to introduce some fundamental tools in the study of manifolds with a lower bound on Ricci curvature. We will first state and prove the laplacian comparison theorem for manifolds with a lower bound on the Ricci curvature, and derive some important consequences : Bishop-Gromov inequality, Myers theorem, Cheeger-Gromoll splitting theorem. Then we will define the Gromov-Hausdorff distance between metric spaces which will allow us to consider limits of sequences of Riemannian manifolds, along the way we will prove Gromov’s precompactness theorem for sequences of manifolds with a Ricci lower bound. We will also see on examples what type of degeneration can occur when considering these « Ricci limit spaces », we will in particular encounter curvature blow up and volume collapsing. One of the major point in the study of these limit spaces is to understand which results on smooth manifolds with a Ricci lower bound carry on to the limit spaces, we will give an introduction to this topic by outlining the proof by Cheeger.