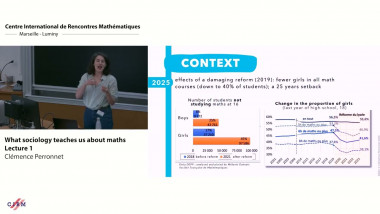
Group actions on quiver moduli spaces and applications
We study two types of actions on King’s moduli spaces of quiver representations over a field k, and we decompose their fixed loci using group cohomology in order to give modular interpretations of the components. The first type of action arises by considering finite groups of quiver automorphisms. The second is the absolute Galois group of a perfect field k acting on the points of this quiver moduli space valued in an algebraic closure of k; the fixed locus is the set of k-rational points, which we decompose using the Brauer group of k, and we describe the rational points as quiver representations over central division algebras over k. Over the field of complex numbers, we describe the symplectic and holomorphic geometry of these fixed loci in hyperkaehler quiver varieties using the language of branes. Over the reals, the rational points of these quiver moduli spaces come from either real or quaternionic quiver representations, and we compute the Poincaré polynomials of both components. This is joint work with Florent Schaffhauser.