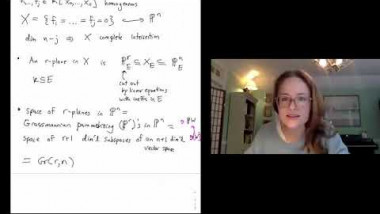
$\mathbb A^1$-Euler numbers can be constructed with Hochschild homology, self-duality of Koszul complexes, pushforwards in $SL_c$ oriented cohomology theories, and sums of local degrees. We show an integrality result for $\mathbb A^1$-Euler numbers and apply this to the enumeration of $d$-planes in complete intersections. Classically such counts are valid over the complex numbers and sometimes extended to the real numbers. $\mathbb A^1$-homotopy theory allows one to perform counts over arbitrary fields, and records information about the arithmetic and geometry of the solutions with bilinear forms. For example, it then follows from work of Finashin–Kharlamov that there are 160;839⟨1⟩+160;650⟨-1⟩ 3-planes in any 7-dimensional cubic hypersurface when these 3-planes are counted with an appropriate weight. This is joint work with Tom Bachmann.