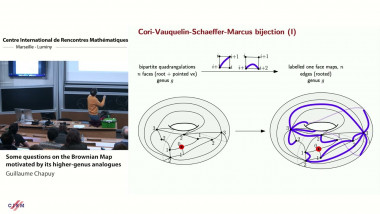
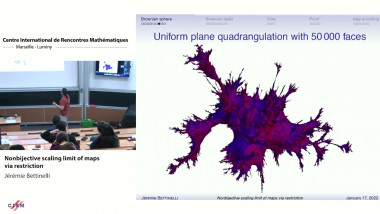
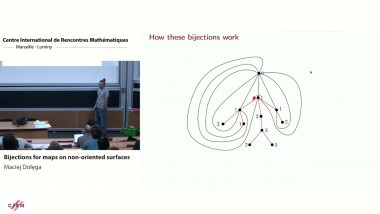
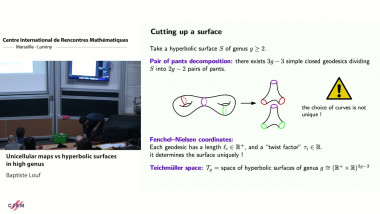
Conformal bootstrap in Liouville theory
Liouville conformal field theory (LCFT) was introduced by Polyakov in 1981 as an essential ingredient in his path integral construction of string theory. Since then Liouville theory has appeared in a wide variety of contexts ranging from random conformal geometry to 4d Yang-Mills theory with supersymmetry. Recently, a probabilistic construction of LCFT on general Riemann surfaces was provided using the 2d Gaussian Free Field. This construction can be seen as a rigorous construction of the 2d path integral introduced in Polyakov's 1981 work. In contrast to this construction, modern conformal field theory is based on representation theory and the so-called bootstrap procedure (based on recursive techniques) introduced in 1984 by Belavin-Polyakov-Zamolodchikov. In particular, a bootstrap construction for LCFT has been proposed in the mid 90's by Dorn-Otto-Zamolodchikov-Zamolodchikov (DOZZ) on the sphere. The aim of this talk is to review a recent series of work which shows the equivalence between the probabilistic construction and the bootstrap construction of LCFT on general Riemann surfaces. In particular, the equivalence is based on showing that LCFT satisfies a set of natural geometric axioms known as Segal's axioms. Based on joint works with F. David, C. Guillarmou, A. Kupiainen, R. Rhodes.