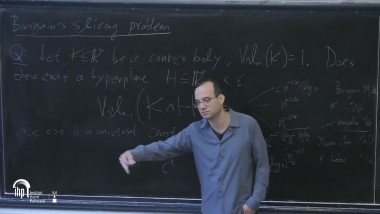This IHP school will focus on advancements from the last 3-4 years in Bourgain's slicing problem and the isoperimetric conjecture proposed by Kannan, Lovasz and Simonovits (KLS). The slicing problem by Bourgain is an innocent-looking question in convex geometry. It asks whether any convex body of volume one in an n-dimensional Euclidean space admits a hyperplane section whose (n-1)-dimensional volume is at least some universal constant. There are several equivalent formulations and implications of this conjecture, which occupies a rather central role in the field. The slicing conjecture would follow from the KLS isoperimetric conjecture, which suggests that the most efficient way to partition a convex body into two parts of equal volume so as to minimize their interface, is a hyperplane bisection, up to a universal constant. Presently, these two conjectures are known to hold true up to factors that increase logarithmically with the dimension.