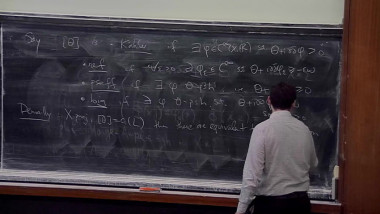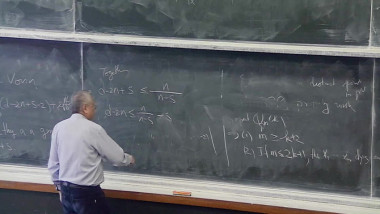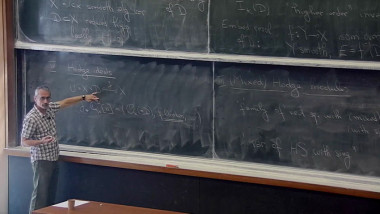One usually considers wave equations as evolution equations, i.e. imposes initial data and solves them. Equivalently, one can consider the forward and backward solution operators for the wave equation; these solve an equation Lu=f, for say f compactly supported, by demanding that u is supported at points which are reachable by forward, respectively backward, time-like or light-like curves. This property corresponds to causality. But it has been known for a long time that in certain settings, such as Minkowski space, there are other ways of solving wave equations, namely the Feynman and anti-Feynman solution operators (propagators). I will explain a general setup in which all of these propagators are inverses of the wave operator on appropriate function spaces, and also mention positivity properties, and the connection to spectral and scattering theory in Riemannian settings, as well as to the classical parametrix construction of Duistermaat and Hörmander.