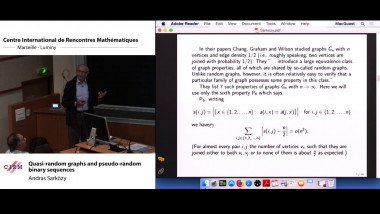
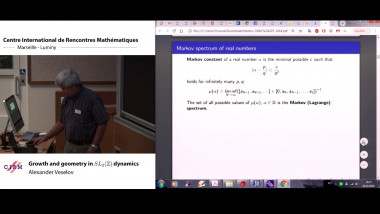
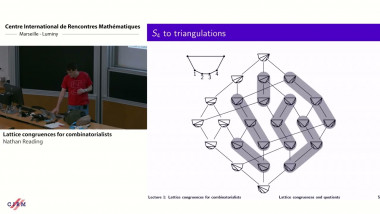
Usual discrete dynamics can be considered as the action of the group of integers. What happens if we replace $\mathbb{Z}$ by $SL_2(\mathbb{Z})$?
There is a classical example of such dynamics goes back to remarkable work by Andrei A. Markov (1880), who described the solutions of the Diophantine equation $x^2 + y^2 + z^2 = 3xyz$ (known now as Markov triples) as an orbit of $SL_2(\mathbb{Z})$. These triples surprisingly appeared in many areas of mathematics: initially in arithmetic, but more recently in hyperbolic and algebraic geometry, the theory of Teichmüller spaces, Frobenius manifolds and Painlevé equations.
Another example of such dynamics appears in the description of the values of a binary quadratic form $Q(x,y) = ax^2+bxy+cy^2$ with integer coefficients, the problem going back to Gauss. About 20 years ago John H. Conway proposed a ”topographic” approach to this problem, using the planar trivalent tree, which can be considered as a discrete version of the hyperbolic plane.
The same approach can be applied to general $SL_2(\mathbb{Z})$ dynamics, and in particular to Markov dynamics as well. The growth of the corresponding numbers depends on the paths on such tree, which can be labelled by the points of real projective line.
I will discuss some results about the corresponding Lyapunov exponents found jointly with K. Spalding and A. Sorrentino, using the known links with the hyperbolic geometry.
